Переходные процессы в несинусоидальных цепях
Переходные процессы в несинусоидальных цепях
Курсовая работа
Выполнил студент гр. 357-2 Карташов В. А.
ТУСУР, Кафедра ТОЭ
Томск 1999
Введение.
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
![]() Гн
Гн
![]() мкФ
мкФ
![]() в
в
![]()
![]()
![]()
![]()
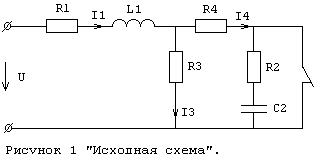
1 Расчет переходного процесса в цепи при постоянном воздействии.
Расчет граничных условий.
А) ![]() (ключ замкнут)
(ключ замкнут)
![]() ;
; 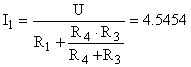 А
А
Б) ![]() (ключ разомкнут)
(ключ разомкнут)
Независимые начальные условия:
![]() ;
; ![]() Согласно закону
коммутации.
Согласно закону
коммутации.
В)![]()
![]() (ключ разомкнут)
(ключ разомкнут)
![]()
![]()
Зависимые начальные условия:
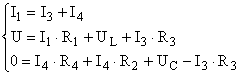 (1)
(1)
В систему (1) подставляем ![]() ,
, ![]() и находим
и находим ![]() ,
, ![]() ,
, ![]()
![]() В
В ![]() А
А ![]() А
А
 Г)
Г) ![]() (ключ разомкнут)
(ключ разомкнут)
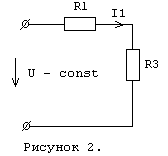
В послекоммутационном режиме схема изображена на рисунке 2.
Находим токи ![]() ,
, ![]() и
и ![]() .
.
![]() А
А ![]()
![]()
![]() в
в
Таблица 1. “Граничные условия”
|
|
|
|
|
|
|
|
|
4.5454 |
3.7879 |
0.7576 |
0 |
-21.2121 |
|
|
3.3333 |
3.3333 |
0 |
66.6666 |
0 |
Расчёт ![]()
![]() ,
,![]() и
и ![]() классическим методом.
классическим методом.
Составляем систему уравнений по законам Кирхкгоффа для схемы
(Рис 1) в момент коммутации.
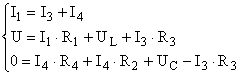
Выразим ![]() через
через ![]() ,
, ![]() и воспользуемся
формулами:
и воспользуемся
формулами:
![]() ;
; ![]() .
.
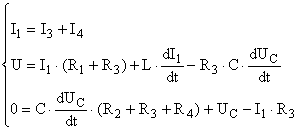
Из третьего уравнения выразим ![]() , найдём
, найдём ![]() и подставим в второе.
и подставим в второе.
Для упрощения выражения подставим константы.
![]()
Решая характеристическое уравнение ![]()
получаем корни ![]()
![]()
![]()
![]()
Общий вид ![]() :
: ![]() , в этом уравнении две неизвестных величины
, в этом уравнении две неизвестных величины ![]() и
и ![]() поэтому нужно ещё
одно уравнение. Его можно найти если использовать соотношение
поэтому нужно ещё
одно уравнение. Его можно найти если использовать соотношение ![]() .
.
![]() , получаем систему
, получаем систему
уравнений: 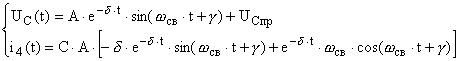 ,
,
воспользуемся граничными условиями при t=0:
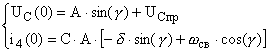
подставив в систему известные константы выразим А из первого
уравнения и подставив во второе найдем ![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() 5;
5;
![]()
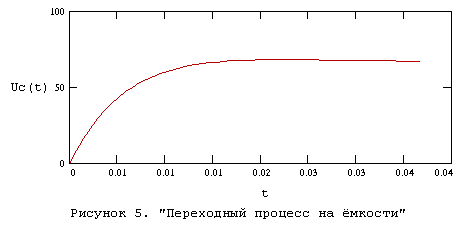
Переходный процесс на рисунке 5 изображен в период времени от 0 до
![]() , где
, где ![]() .
.
1.3 Расчёт ![]()
![]() и
и ![]() методом входного
сопротивления.
методом входного
сопротивления.
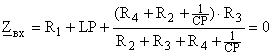
Внеся всё под общий знаменатель и приравняв числитель к нулю, получаем квадратное уравнение
относительно P.
![]()
Его решением являются корни ![]()
![]()
![]()
![]()
Рассчёт тока ![]() операторным методом.
операторным методом.
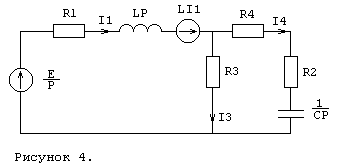
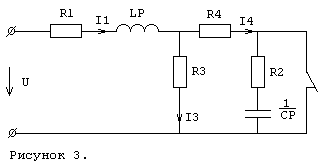
Схема преобразованая для рассчёта операторным методом
изображена на рисунке 4.
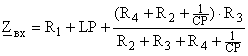
![]()
![]()
![]()
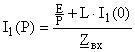 ;
; 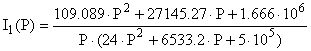
Выражение для тока имеет вид ![]() , оригинал будем искать в виде функции
, оригинал будем искать в виде функции ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Подставив все в выражение для тока получаем:
![]()
Расчет переходного процесса в цепи при гармоническом воздействии.
2.1 Расчёт граничных условий.
А) ![]() (ключ замкнут)
(ключ замкнут)
![]() Ом;
Ом; ![]() Ом
Ом
![]() ;
; 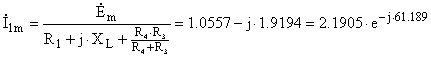 А
А
![]() А;
А; ![]()
Б) ![]() (ключ разомкнут)
(ключ разомкнут)
Независимые начальные условия:
![]() ;
; ![]() Согласно закону
коммутации.
Согласно закону
коммутации.
В)![]()
![]() (ключ разомкнут)
(ключ разомкнут)
![]()
![]()
Зависимые начальные условия:
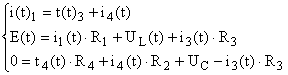 (1)
(1)
В систему (1) подставляем ![]() ,
, ![]() и находим
и находим ![]() ,
, ![]() ,
, ![]()
![]() В
В ![]() А
А ![]() А
А
Г) ![]() (ключ разомкнут)
(ключ разомкнут)
Находим токи ![]() ,
, ![]() и
и ![]() .
.
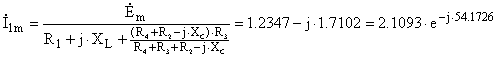
![]()
![]()
![]()
![]() А
А
![]()
![]() ;
; ![]() В
В
Таблица 2. “Граничные условия”
|
|
|
|
|
|
|
|
|
-1.9194 |
-1.5984 |
-0.3196 |
0 |
51.148 |
Нахождение ![]() классическим методом.
классическим методом.
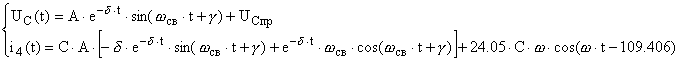
Воспользуемся граничными условиями.
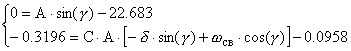
![]()
![]()
![]() ;
; ![]()
![]()
Переходный процесс на конденсаторе при гармоническом воздействии изображён на рисунке 6.
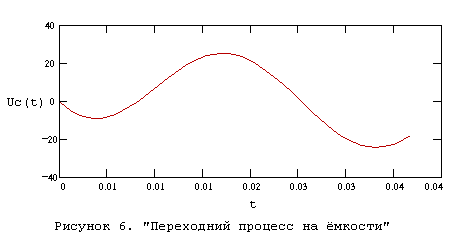
Расчет переходного процесса в цепи при несинусоидальном воздействии.
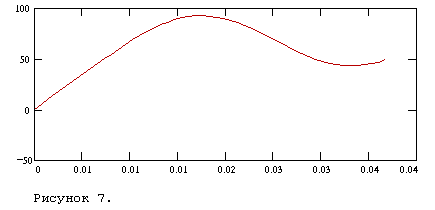
Так как схема является линейной, выполняется закон суперпозиции.
Эту схему можно рассчитать методом наложения, т.е. для нахождения
![]() при несинусоидальном
воздействии достаточно сложить ранее найденные
при несинусоидальном
воздействии достаточно сложить ранее найденные ![]() при постоянном
воздействии и
при постоянном
воздействии и ![]() при синусоидальном
воздействии.
при синусоидальном
воздействии.
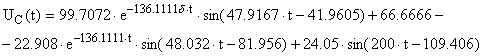
Анализ зависимости типа переходного процесса в цепи от одного линейного параметра.
Если в исходной схеме мы уменьшим ёмкость конденсатора в два раза то корни характеристического уравнения будут иными:
![]()
![]() - действительными,
разными.
- действительными,
разными.
Следовательно переходный процесс в этой цепи будет носить апериодический характер.
Дата добавления: 30.10.2004


