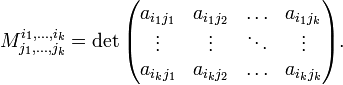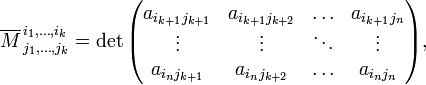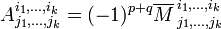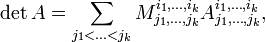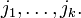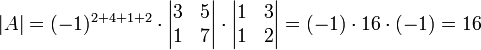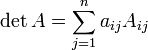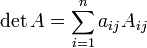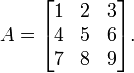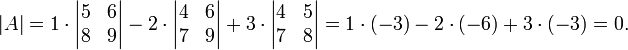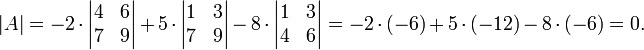Теорема Лапласа

Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.

Формулировка

Для начала, введём несколько определений.

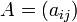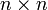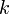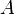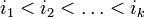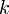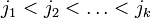Пусть $A=(a_{ij})$ — матрица размера $n \times n$ , и пусть выбраны любые $k$ строк матрицы $A$ с номерами $i_1 < i_2 < \ldots < i_k$ и любые $k$ столбцов с номерами $j_1 < j_2 < \ldots < j_k$ .

Определитель матрицы, получаемой из 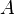$A$ вычеркиванием всех строк и столбцов, кроме выбранных, называется минором 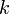$k$ -го порядка, расположенным в строках с номерами 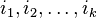$i_1, i_2, \ldots, i_k$ и столбцах с номерами 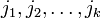$j_1, j_2, \ldots, j_k$ . Он обозначается следующим образом:

$M^{i_1,\ldots,i_k}_{j_1,\ldots,j_k} = \det \begin{pmatrix} a_{i_1 j_1} & a_{i_1 j_2} & \ldots & a_{i_1 j_k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i_k j_1} & a_{i_k j_2} & \ldots & a_{i_k j_k} \end{pmatrix}.$

А определитель матрицы, получаемой вычеркиванием только выбранных строк и столбцов из квадратной матрицы, называется дополнительным минором к минору 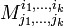$M^{i_1,\ldots,i_k}_{j_1,\ldots,j_k}$ :

$\overline{M}^{\,i_1,\ldots,i_k}_{\,j_1,\ldots,j_k} = \det \begin{pmatrix} a_{i_{k+1} j_{k+1}} & a_{i_{k+1} j_{k+2}} & \ldots & a_{i_{k+1} j_n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i_n j_{k+1}} & a_{i_n j_{k+2}} & \ldots & a_{i_n j_n} \end{pmatrix},$

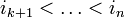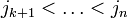где $i_{k+1} < \ldots < i_n$ и $j_{k+1} < \ldots < j_n$ — номера невыбранных строк и стобцов.

Алгебраическое дополнение минора 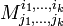$M^{i_1,\ldots,i_k}_{j_1,\ldots,j_k}$ определяется следующим образом:

$A^{i_1,\ldots,i_k}_{j_1,\ldots,j_k} = (-1)^{p+q} \overline{M}^{\,i_1,\ldots,i_k}_{\,j_1,\ldots,j_k}$

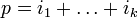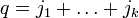где $p = i_1 + \ldots + i_k$ , $q = j_1 + \ldots + j_k$ .

Справедливо следующее утверждение.

Теорема Лапласа

Пусть выбраны любые $k$ строк матрицы $A$ . Тогда определитель матрицы $A$ равен сумме всевозможных произведений миноров $k$ -го порядка, расположенных в этих строках, на их алгебраические дополнения.

$\det A = \sum_{j_1<\ldots<j_k}M^{i_1,\ldots,i_k}_{j_1,\ldots,j_k} A^{i_1,\ldots,i_k}_{j_1,\ldots,j_k},$

где суммирование ведётся по всевозможным номерам столбцов $j_1, \ldots, j_k.$

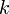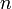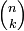Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать $k$ столбцов из $n$ , то есть биномиальному коэффициенту $\textstyle {n \choose k}$ .

Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.

Примеры

Рассмотрим квадратную матрицу

$A = \begin{bmatrix} 5 & 9 & 1 & 3 \\ 3 & 5 & 0 & 0 \\ 67 & 932 & 1 & 2 \\ 1 & 7 & 0 & 0 \end{bmatrix}.$

Выберем вторую и четвертую строки и разложим определитель этой матрицы по теореме Лапласа. Заметим, что в этих строках все миноры второго порядка, кроме $\begin{vmatrix} 3 & 5 \\ 1 & 7 \end{vmatrix}$ , содержат нулевые столбцы, т.е. заведомо равны нулю и на сумму в теореме не влияют. Поэтому определитель будет равен:

$|A| = (-1)^{2+4+1+2}\cdot\begin{vmatrix} 3 & 5 \\ 1 & 7 \end{vmatrix}\cdot\begin{vmatrix} 1 & 3 \\ 1 & 2 \end{vmatrix} = (-1)\cdot16\cdot(-1) = 16$

Из приведенного примера видно, что теорема Лапласа упрощает вычисление определителей не всех матриц, а только матриц особого вида. Поэтому на практике чаще используются другие методы, например, метод Гаусса. Теорема больше применяется для теоретических исследований

Разложение определителя по строке (столбцу) (Следствие 1)

Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.

Пусть 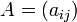$A = (a_{ij})$ — квадратная матрица размера 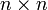$n \times n$ . Пусть также задан некоторый номер строки 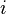$i$ либо номер столбца 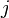$j$ матрицы 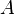$A$ . Тогда определитель 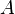$A$ может быть вычислен по следующим формулам:

Разложение по $i$ -й строке:

$\det A = \sum_{j=1}^n a_{ij} A_{ij}$

Разложение по $j$ -му столбцу:

$\det A = \sum_{i=1}^n a_{ij} A_{ij}$

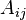где $A_{ij}$ — алгебраическое дополнение к минору, расположенному в строке с номером 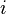$i$ и столбце с номером 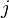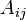$j$ . $A_{ij}$ также называют алгебраическим дополнением к элементу $a_{ij}$ .

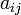Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить 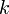$k$ равным 1 и выбрать 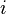$i$ -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.

ассмотрим квадратную матрицу

$A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}.$

Разложим определитель по элементам первой строки матрицы:

$|A| = 1 \cdot \begin{vmatrix} 5 & 6 \\ 8 & 9 \end{vmatrix} - 2 \cdot \begin{vmatrix} 4 & 6 \\ 7 & 9 \end{vmatrix} + 3 \cdot \begin{vmatrix} 4 & 5 \\ 7 & 8 \end{vmatrix} = 1 \cdot (-3) - 2 \cdot (-6) + 3 \cdot (-3) = 0.$

(Обратите внимание, что у алгебраического дополнения ко второму элементу первой строки отрицательный знак).

Также определитель можно разложить, например, по элементам второго столбца:

$|A| = -2 \cdot \begin{vmatrix} 4 & 6 \\ 7 & 9 \end{vmatrix} + 5 \cdot \begin{vmatrix} 1 & 3 \\ 7 & 9 \end{vmatrix} - 8 \cdot \begin{vmatrix} 1 & 3 \\ 4 & 6 \end{vmatrix} = -2 \cdot (-6) + 5 \cdot (-12) - 8 \cdot (-6) = 0.$

Следствие 2 (фальшивое разложение определителя)

Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.

Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0 . С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матри- цы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А.

Примечания

↑ Smith, D. E. Project Gutenberg’s History of Modern Mathematics. — P. 18.

Список литературы

Ильин, В. А., Позняк, Э. Г. Линейная алгебра. — 6-е изд. — М.: Физматлит, 2005. — С. 25-27. — ISBN 5-9221-0481-0
Прасолов, В. В. Задачи и теоремы линейной алгебры. — 2-е изд. — М., 2008. — С. 42-45.

Для подготовки данной работы были использованы материалы с сайта http://ru.wikipedia.org/

Дата добавления: 14.12.2012

Поиск по рефератам и авторским статьям

Теорема Лапласа

Разложение определителя по строке (столбцу) (Следствие 1)

Следствие 2 (фальшивое разложение определителя)

Примечания