Элементарное доказательство иррациональности числа e
Конечно же, “элементарность’’ данного доказательства относительна. Однако оно должно быть понятно студенту первого курса вуза, изучающему высшую математику.
Будем доказывать от противного. Предположим, что
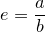 ,
,
где 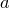 и
и 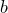 — натуральные числа.
— натуральные числа.
Учитывая данное равенство и рассматривая разложение 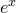 в ряд:
в ряд:
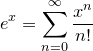 ,
,
получаем следующее равенство:
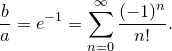
Представим данную сумму в виде суммы двух слагаемых, одно из которых — сумма членов ряда по 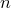 от
от 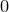 до
до 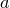 , а второе — сумма всех остальных членов ряда:
, а второе — сумма всех остальных членов ряда:
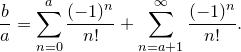
Теперь перенесем первую сумму в левую часть равенства:
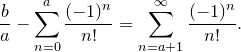
Умножим обе части полученного равенства на 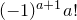 . Получим
. Получим
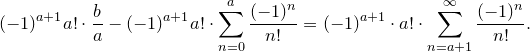
Теперь упростим полученное выражение:
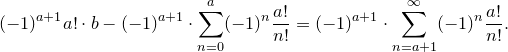
Рассмотрим левую часть полученного равенства. Очевидно, что число 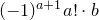 целое. Целым является также и число
целое. Целым является также и число 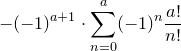 , поскольку
, поскольку 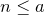 (отсюда следует, что все числа вида
(отсюда следует, что все числа вида 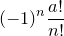 целые). Тем самым левая часть полученного равенства — целое число.
целые). Тем самым левая часть полученного равенства — целое число.
Перейдем теперь к правой части. Эта сумма имеет вид
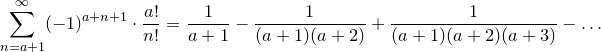
По признаку Лейбница этот ряд сходится, и его сумма 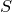 есть вещественной число, заключенное между первым слагаемым и суммой первых двух слагаемых (со знаками), т.е.
есть вещественной число, заключенное между первым слагаемым и суммой первых двух слагаемых (со знаками), т.е.
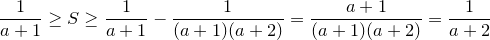 .
.
Оба эти числа при 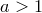 лежат между
лежат между 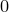 и
и 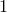 . Следовательно,
. Следовательно, 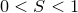 , т.е.
, т.е. 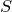 — правая часть равенства — не может быть целым числом. Получили противоречие: целое число не может быть равно числу, которое не является целым.
— правая часть равенства — не может быть целым числом. Получили противоречие: целое число не может быть равно числу, которое не является целым.
Это противоречие доказывает, что число  не является рациональным.
не является рациональным.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://hijos.ru/
Дата добавления: 11.04.2013


