Дискретная модель пространства-времени ограниченная предельной скоростью распространения сигналов с и неравенством В. Гейзенберга с постоянной h

 

Cалагаева Анжелика Валериевна, кандидат технических наук

Хлебопрос Р.Г., Сибирский федеральный университет, кафедра экономики и природопользования, профессор, доктор физико-математических наук

Введение

К настоящему времени появилось множество работ [1–11], в которых предприняты попытки построения дискретной модели пространства-времени. Очевидно, что в этом случае должны выполнятся неравенства, обусловленные предельной скоростью распространения сигналов с и принципом неопределенности с постоянной h. В данной случае рассматривается проблема дискретного пространства-времени с учетом указанных ограничений.

Результаты

Deltax<=cDeltat,                                                (1)

Deltat>=Deltax/c.                                                (2)

Примем c=1, и запишем неравенство Гейзенберга для релятивистского случая [13]:

DeltapDeltax>= ħ.                                               (3)

Положим, что Deltap~~dp, и

dp=mdv/root(3/2)(1-beta^(2)),                                                  (4)

гдеbeta=v/c, dv=Deltav=Deltax/Deltat. Тогда,

mDeltax^(2)/(1-beta^(2))^(2)Deltat>=ħ.                              (5)

Выразивиз(5) Deltat, имеем

Deltat<=mDeltax^(2)/(1-beta^(2))^(2)ħ.                              (6)

Обозначим величинуħ/mкак tau. Тогда выражение (6) запишется следующим образом:

Deltat<=Deltax^(2)/ tau(1-beta^(2))^(2).                              (7)

На Рис. 1 изображена зависимость Deltat(Deltax). В области, расположенной левее точки (в данном случае практически вся заштрихованная область, приведенная на Рис. 1 подлежит дискретизации, точка пересечения принадлежит только большим значениям Deltat) пересечения прямой beta=const с параболой Deltat(Deltax) возможна дискретизация пространства-времени вследствие проявления квантовых эффектов. Дискретизация пространства-времени допустима при условии, если tau(1-beta^(2))^(2)>>1.Область (см. Рис. 1), расположенная правее точки пересечения прямой beta=const с параболой Deltat(Deltax) соответствует обычной релятивистской, или в случае малых скоростей, ньютоновской механике. Данную область можно рассматривать как континуум.Рис. 1. Область дискретного (заштрихованная область) и сплошного времени.

 

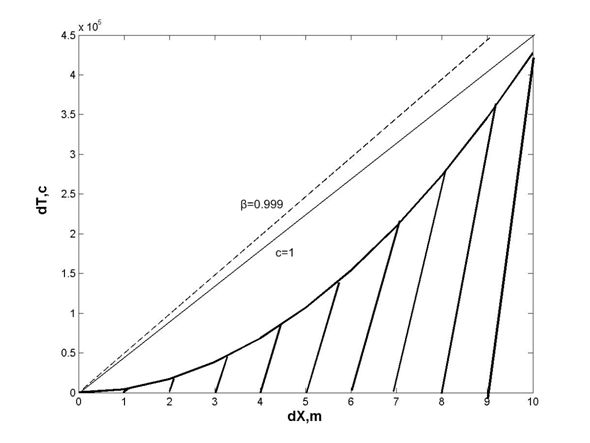
 Рис. 1. Дискретные (заштрихованные) и сплошные временные области

Теперь рассмотрим зависимость Deltax от Deltat. Из (5) выразим Deltax:

Deltax>=sqrt(ħDeltat/m)(1-beta^(2))                                            (8)

или

Deltax>=sqrt(tauDeltat)(1-beta^(2)).                                             (9)

 

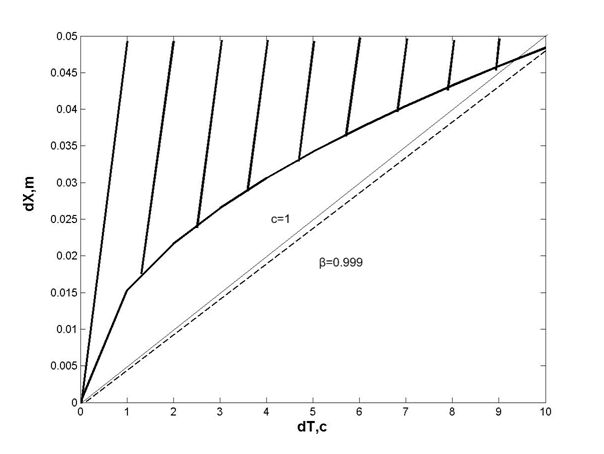
Рис. 2. Область дискретного (заштрихованная область) и сплошного пространства.

На Рис. 2 представлена зависимость Deltax от Deltat. В данном случае дискретность пространства-времени проявляется, если sqrt(tau)(1-beta^(2))>>1. Область правее точки пересечения прямой beta=const с кривой Deltax(Deltat) соответствует обычной релятивистской (в случае малых скоростей ньютоновской) механике.Указанные условия выполняются при сравнительно малых скоростях, beta<1,и малых массах, m<=mкр.

Выводы

Таким образом, исходя из полученных неравенств, имеем дискретные и сплошные временные и пространственные интервалы. Видно, что с увеличением массы и скорости область сплошных временных и пространственных интервалов увеличивается. Для макроскопических объектов практически весь временной интервал является сплошным, и дискретность времени никак не проявляется. Кроме того, неравенство Гейзенберга остается в силе в процессе инфляционного расширения вселенной, когда могут нарушаться ограничения СТО, что необходимо учитывать при построении космологических моделей.

Список литературы

1. R. Fürth, Nw (17), 668–669, (1929).

2. R. Fürth, Zph (57), 429–446, (1929).

3. I. Watanabe, PTPh (24), 465–483, (1960).

4. Alain Aspect, Bell's Theorem: The naive view of an experimentalist, Springer (2002).

5. D. Bom, Quantum Theory, New York: Prentice Hall, (1951).

6. Hugh Everett, Reviews of Modern Physics (vol 29), 454—462, (1957).

7. В.Л. Янчилин, Квантовая нелокальность, Москва, (2009).

8. А.Н. Вяльцев, Дискретное пространство-время, Москва, (2007).

9. P. Forrest, Synthese 103 (3), 327 (1995).

10. B. Gaveau, T. Jacobson, M. Kac and L. S. Schulman, Phys. Rev. Lett. 53, 419 (1984).

11. С.Г. Рубин, К.А.Бронников, Лекции по гравитации и космологии, Москва, (2008).

12. Л.Д Ландау, Е.М. Лившиц, Курс теоретической физики, т. 2., Теория поля, Москва (1988).

13. Л.Д Ландау, Е.М. Лившиц, Курс теоретической физики, т. 4., Квантовая электродинамика, Москва (2001).

Для подготовки данной работы были использованы материалы с сайта http://www.all-fizika.com/

Дата добавления: 21.05.2014