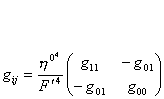Отображение геометрических структур
Mapping geometrical arrangements of a fiber space of differential equations, bound mapping of Hopf-Colle is under construction.
Устанавливается изоморфизм отображений Хопфа-Коула (Hopf E, Cole J. D.) [ 1, 2 3 ] и отображений геометрических структур дифференциальных уравнений, что позволяет определить сферы действия геометрического исчисления с соответствующей метрикой. Эта сфера действия соответствующих метрик определяется линейными и нелинейными связями.
Имеется проблема.
В настоящее время геометрии искривленных пространств позволяют извлекать физическую информацию в основном о системах космических и галактических масштабов: релятивистская теория гравитации (ОТО) и новая релятивистская теория гравитации (РТГ), в которых определяется «метрический тензор риманового пространства».
Но геометрия – раздел математики. Геометрическое исчисление имеет силу во всех разделах физики. Примером может служить интегральное исчисление, которое широко используется во всех разделах физики.
С помощью метрического тензора опускают и поднимают индексы у тензоров, находят их абсолютные переносы, определяют ковариантные производные и связности… Итак, посредством определенных в ОТО и РТГ метрических тензоров дважды поднимаются индексы, например, у тензора диэлектрической проницаемости в электродинамике, определяется перенос составляющих вектора электрической напряженности. Каков физический смысл этих действий? Ведь метрические тензоры в ОТО и РТГ – это гравитационные потенциалы!
В материальном мире реализуются многомерные пространства. С каждой физической системой и с каждым процессом ассоциируются соответствующей структуры пространства. Введение многомерных расслоенных пространств возможно во всех разделах физики. И не просто возможно, а геометрии расслоенных пространств составляют основу теорий всех разделов физики.
Геометрические действия с соответствующей метрикой возможно только в рамках соответствующей связи. При переходе к другой связи посредством соответствующих отображений происходит переход и к другой метрике посредством этих же отображений. Введение тензоров (скаляров, спиноров, векторов, тензоров более высокого ранга) производится только относительно соответствующих преобразований обобщенных координат. В физике вводятся многомерные пространства внутренних степеней свободы. Примером пространства внутренних степеней свободы в физике может служить изотопическое пространство, векторы в котором вводятся на основе преобразований координат изотопического пространства. В пространстве внутренних степеней свободы вводятся обобщенные базовые и слоевые координаты.
В качестве демонстрации данных утверждений и рассматривается сформулированная здесь задача.
Отображение Хопфа-Коула связывает два дифференциальных уравнения и их решения [ 1, 2, 3 ]: нелинейное уравнение Бюргерса [ 4 ] и уравнение теплопроводности (диффузии). Эти уравнения отображают соответствующие связи. Этих уравнений мы рассматриваем частные случаи (демонстрируется сам принцип) и обобщаем их на слоевые пространства.
Нелинейное уравнение (3) (см. Табл.) получено из уравнения типа уравнения Бюргерса в классе решений
![]()
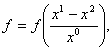 т.е.
т.е. ![]() (1)
(1)
с использованием отображения (2) [ 5 ]:
Отображение геометрических структур
Таблица
|
Дифференциальное уравнение типа уравнения теплопроводности
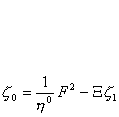
|
Дифференциальные уравнения, связанные отображением Хопфа-Коула
|
Уравнение, следующее из нелинейного дифференциального уравнения типа уравнения Бюргерса
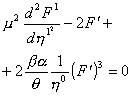
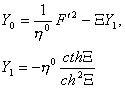 (9) (9)
(11)
|
Из Таблицы следует, что структура составляющих контравариантных векторов, метрического
тензора, связностей сохраняется. Изменяется их конкретное содержание. Отображения Хопфа-Коула меняют длину слоевых координат ![]() . Поскольку выполняется условие Эйлера и сохраняется свойство (14),то коэффициенты связностей найдены правильно. Итак, 1)если связь задана
дифференциальным уравнением вида (3), тогда следует проводить геометрическое исчисление с метрическим тензором (10) и метрикой (5), 2)если же связь задана
нелинейным дифференциальным уравнением вида (4), тогда следует проводить геометрическое исчисление
с метрическим тензором (11) и метрикой (6), которые могут быть получены отображением Хопфа-Коула (2).
. Поскольку выполняется условие Эйлера и сохраняется свойство (14),то коэффициенты связностей найдены правильно. Итак, 1)если связь задана
дифференциальным уравнением вида (3), тогда следует проводить геометрическое исчисление с метрическим тензором (10) и метрикой (5), 2)если же связь задана
нелинейным дифференциальным уравнением вида (4), тогда следует проводить геометрическое исчисление
с метрическим тензором (11) и метрикой (6), которые могут быть получены отображением Хопфа-Коула (2).
ЛИТЕРАТУРА
1.Cole J.D. On a quasilinear parabolic equation occurring in aerodynamics/ Quart App. Vath.,1951, 9, pp. 225-236.
2.Hopf T. The partial differential equation ![]() Comm. Pure
Appl.Math.,1950, pp/ 201-230.
Comm. Pure
Appl.Math.,1950, pp/ 201-230.
3.Абловиц М., Сигур X. Солитоны и метод обратной задачи. Перевод с англ. -М.: Мир, 1987, 180 с.
4.Burgers J. M. A mathematical model illustrating the theory of turbulence/Adv. Appl. Mech, 1948, 1, pp. 171-199.
5.Севрюк В.П. Геометрии расслоенных пространств теории обобщенных криволинейных координат. ВИНИТИ , N 3378-B90 Деп., 145 с.


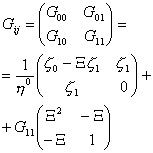 (10)
(10)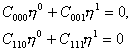
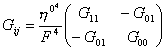
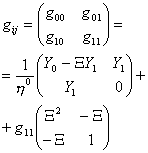
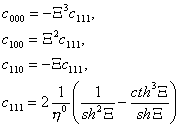 (13)
(13)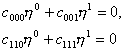 )
)