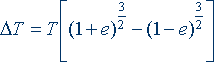Кольцевой орбитальный резонанс

Кольцевой орбитальный резонанс

Кирилл Бутусов

В 1978 г. нами была опубликована работа «Золотое сечение в Солнечной системе» [1], где было показано, что в Солнечной системе наблюдается явление резонанса волн биений, приводящее к тому, что периоды и частоты обращений планет образуют геометрическую прогрессию со знаменателями Ф = 1,6180339 и Ф = 2,6180339, хорошо отображаемые числовыми рядами: Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...) и Люка (2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843...), см. табл. 1, где n – числа Люка и Фибоначчи, а δ% – отклонение от резонансного значения nT в %.

Таблица 1

Тело	Т, лет	n	nT, лет	δ%
Ме	0,24085	377	90,800	1,98
В	0,61521	144	88,590	0,50
З	1,00000	89	89,000	0,03
Ма	1,88089	47	88,401	0,71
С	29,4577	3	88,373	0,74
			89,033	0,79
Ц	4,605	18	82,893	0,10
Ю	11,862	7	83,035	0,06
У	84,015	1	84,015	1,24
Н	164,78	1/2	82,394	0,71
П	247,69	1/3	82,565	0,50
			82,980	0,52

Однако, кроме описанных в статье случаев проявления «золотого сечения» в Солнечной системе, нам удалось выявить ещё ряд новых интересных примеров такого же рода. В частности, мы обнаружили, что величины, обратные эксцентриситетам планетных орбит также близки к числам Люка и Фибоначчи (см. табл. 2, где e – эксцентриситет орбиты, а n – число Люка или Фибоначчи).

Таблица 2

Тело	1/e	n	1/ne	δ%
П	4,021	4	1,0054	0,44
Ме	4,863	5	0,9726	2,91
Ма	10,711	11	0,9737	2,80
Ц	13,157	13	1,0121	1,10
С	17,946	18	0,9970	0,40
Ю	20,652	21	0,9834	1,79
У	21,195	21	1,0093	0,82
З	59,772	55	1,0867	8,56
Н	116,686	123	0,9486	5,52
В	147,058	144	1,0212	2,01
			1,0010	2,63

Так как орбиты планет эллиптичны и постепенно прецессируют, то каждая из них занимает кольцевую область между двумя круговыми орбитами с радиусами:

r_π = (1 – e)a	(1)
r_α = (1 + e)a	(2)

где r_π – радиус орбиты в перигелии,

r_α – радиус орбиты в афелии,

a – большая полуось орбиты.

Этим круговым орбитам соответствуют свои периоды, а интервал периодов может быть найден по следующей формуле:

(3)

где T – период обращения планеты, а ΔT – будет шириной орбиты, выраженной в терминах периодов. Назовем эту величину «периодом ширины орбиты». При этом оказалось, что «период ширины орбиты» связан с перодом обращения планеты, расположенной через одну орбиту ближе к Солнцу, следующим соотношением:

kΔT_n = T_n–2 ,

(4)

где k – целое число, чаще всего, близкое к единице, т.е. имеет место своеобразный резонанс, названный нами «кольцевым резонансом» (см. табл. 3).

Таблица 3а

Тело	ΔT, лет	k	kΔT_n, лет
В	0,0125	5	0,0627
З	0,0501	5	0,2509
М	0,5266	1	0,5266
Ц	1,0497	1	1,0497
Ю	1,7228	1	1,7228
С	4,9235	1	4,9235
У	11,890	1	11,890
Н	4,237	7	29,659
П	184,28	0,5	92,140

Таблица 3b

Teло	T, лет	kΔT_n / kΔT_n–2	δ%	k	kΔT_n / kΔT_n–2	δ%
Сл	0,0694	0,903	10,0	11/2	0,993	0,61
Ме	0,2408	1,041	4,8	24/5	1,000	0,07
В	0,6152	0,855	16,0	7/6	0,998	0,08
З	1,0000	1,049	5,6	20/21	0,999	0,02
Ма	1,8808	0,915	8,4	12/11	0,999	0,02
Ц	4,6052	1,069	7,6	14/15	0,997	0,16
Ю	11,862	1,002	0,8	1/1	1,002	0,28
Ст	29,457	1,006	1,3	7/1	1,006	0,73
У	84,015	1,096	10,3	5/11	0,997	0,24
		0,993	7,2		0,999	0,24

Как видно из таблицы, при грубой подборке коэфициента k он чаще всего принимает значение 1 и даёт отклонение от резонансности, равное 7,2%, а при более тонкой подборке коэфициента, когда он не целочислен, но равен отношению небольших чисел, это отклонение имеет величину только 0,24%. Учитывая, что на самом деле мгновенный период обращения планеты меняется в широких пределах, можно считать, что резонанс всегда соблюдается даже при грубой подборке k. Как оказалось, экваториальный период вращения Солнца и все «периоды ширины орбит» планет земной группы имеют между собою общий резонанс. Для планет, внешних по отношению к Земной орбите также имеет место общий для них резонанс. Причём средние отклонения от резонансности для обеих групп планет не превышают 0,55%. Период общего резонанса для внешних планет превосходит аналогичный период для земной группы планет в 28 раз (см. табл. 4).

Таблица 4

Тело	ΔT	n	ΔT / n	δ%
В	0,0125	2	0,00627	0,19
З	0,0501	8	0,00627	0.16
Сл	0,0694	11	0,00631	0,86
Ме	0,1483	24	0,00618	1,35
Ма	0,5266	84	0,00627	0,10
			0,00626	0,53
Ма	0,5266	3	0,17553	0,30
Ц	1,0497	6	0,17495	0,02
Ю	1,7228	10	0,17228	1,58
Н	4,2370	24	0,17654	0,88
Ст	4,9235	28	0,17584	0,48
У	11,890	68	0,17485	0,08
			0,17500	0,55

Если рассмотреть ширину орбиты в терминах частот обращений планет, то мы получим «частоту ширины орбиты». Как выяснилось, эти величины, нормированные на «частоту ширины орбиты» Нептуна, образуют числовые ряды, близкие к числам Люка и Фибоначчи (см. табл. 5) со средним отклонением от резонансности меньше 3%.

Таблица 5

Тело	Δν, год^–1	Δν / Δν_Н	n	Δν / nΔν_Н	δ%
Н	0,000156	1,0000	1	1,0000	1,62
У	0,001690	10,8346	11	0,98496	3,17
П	0,003305	21,1871	21	1,00890	0,72
С	0,057000	36,5384	34	1,07465	5,75
Ю	0,012286	78,7564	76	1,03626	1,97
В	0,033516	212,564	199	1,06816	5,11
З	0,050200	321,794	322	0,99936	1,68
Ц	0,049938	320,051	322	0,99394	2,23
Ма	0,150818	966,782	987	0,97951	3,69
				1,01619	2,88

Мы рассматривали до сих пор интервалы периодов и частот, определяемых через радиусы круговых орбит, ограничивающих эллипсы орбит. Однако, интересно рассмотреть разности мгновенных периодов обращения планет в афелиях и перигелиях орбит т.е. интервал, в пределах которого меняется мгновенный период при движении планеты по орбите. Назовём этот интервал «девиацией периода» Расчёт её будем вести по формуле:

(5)

При этом оказалось, что наблюдается резонанс между «девиацией периода» планеты и периодом соседней планеты, расположенной ближе к Солнцу:

kΔT^*_n = T^*_n–1

(6)

См. табл. 6, где значки π, 0, α – определяют значения мгновенных периодов в перигелии, на среднем расстоянии и в афелии. Мы видим, что чаще всего наблюдается k = 2. Среднее отклонение от резонанса равно 1,75%.

Таблица 6

Тело	ΔT_n^*	k	k ΔT_n^*	Тело	T^*_n–1	kΔT^_n / ΔT^_n–1	δ%
Ме	0,2024	1/3	0,0674	Сл_е	0,0694	0,97099	2,58
В	0,0167	9	0,1505	Ме_π	0,1553	0,96968	2,72
З	0,0669	9	0,6023	В_π	0,6068	0,99253	0,35
Ма	0,5442	2	1,0884	З_α	1,0338	1,05279	5,69
Ц	1,4040	4/3	1,8720	Ма₀	1,8808	0,99528	0,08
Ю	2,3000	2	4,6000	Ц₀	4,6052	0,99888	0,28
Ст	6,5757	2	13,1514	Ю_α	13,0539	1,00746	1,14
У	15,8730	2	31,7460	С_α	32,8829	0,96542	3,17
Н	5,6494	15	84,7412	У₀	84,0152	1,00864	1,26
П	254,336	7/11	161,850	Н_π	161,981	0,99919	0,31
						0,99608	1,75

На самом деле, учитывая, что изменение мгновенного периода происходит в широких пределах, мы можем считать, что резонанс всегда соблюдается гораздо точнее.

Наконец, рассмотрим соотношения экстремальных значений мгновенных периодов на соседних орбитах в ближайших апсидах. Например, отношение мгновенного периода в афелии орбиты к такому же периоду, но уже в перигелии последующей орбиты, расположенной дальше от Солнца (см. табл. 7, где T₁^* – мгновенный период в афелии орбиты, а T₂^* – мгновенный период в перигелии последующей). Исключение составляют только Меркурий,где вместо перигелийных и афелийных периодов взяты средние периоды и Венера, где вместо афелийного периода взят средний период. Резонансный коэфициент равен отношению небольших чисел, на 85% состоящих из чисел Люка (2, 3, 4, 7, 11).

Анализ таблицы показывает, что эти соотношения близки к резонансным со средним отклонением от резонансности 0,53%.

Таблица 7

Тело	T₂^*	Тело	T₁^*	k	kT₁^*	T₂^* / kT₁^*	δ%
Ме₀	0,2408	Сл_е	0,0694	7/2	0,2432	0,990304	1,03
В_π	0,6068	Ме₀	0,2408	5/2	0,6021	1,007897	0,73
З_π	0,9669	В₀	0,6152	11/7	0,9667	1,000202	0,03
Ма_π	1,6162	З_α	1,0338	11/7	1,6246	0,994791	0,57
Ц_π	3,9432	Ма_α	2,1604	11/6	3,9608	0,995554	0,50
Ю_π	10,7539	Ц_α	5,3472	2/1	10,6944	1,005564	0,50
Ст_π	26,3072	Ю_α	13,0539	2/1	26,1079	1,007633	0,70
У_π	76,3596	Ст_α	32,8829	7/3	76,7268	0,995213	0,53
Н_π	161,981	У_α	92,2326	7/4	161,407	1,003557	0,30
П_π	144,369	Н_α	167,630	6/7	143,683	1,004770	0,42
						1,000548	0,53

Выводы

Величины, обратные эксцентриситетам орбит планет образуют числа, близкие к числам Люка и Фибоначчи.

Периоды ширины орбитальных колец находятся в резонансе с периодами планет, расположенными через одну орбиту ближе к Солнцу.

Частоты ширины орбитальных колец находятся в резонансе с частотами обращения планет, расположенных дальше от Солнца через одну орбиту.

Периоды ширины орбитальных колец как земной группы планет, так и планет, внешних по отношению к земной орбите, образуют две группы тел с общими резонансами внутри группы.

Частоты ширины орбитальных колец, нормированные на частоту ширины орбиты Нептуна, образуют числовой ряд близкий к числам Люка и Фибоначчи.

Девиации периодов обращений планет находятся в резонансе с периодом обращения соседней планеты, расположенной ближе к Солнцу.

Экстремальные периоды в ближайших апсидах соседних планет находятся в резонансе, а числовые коэфициенты резонансов на 85% состоят из чисел Люка (2, 3, 4, 7, 11).

Имеют место ещё и другие резонансные соотношения для частот ширины орбит, девиаций частоты и экстремальных значений частот планетных орбит, но ввиду ограниченности объёма работы мы этих результатов вычислений не приводим.

Список литературы

К.П. Бутусов. «Золотое сечение в Солнечной системе». Проблемы исследования Вселенной, вып. 7. М.-Л., 1978.

Дата добавления: 18.12.2004

Поиск по рефератам и авторским статьям

Кольцевой орбитальный резонанс