О вычислении коэффициентов и узлов одной квадратурной формулы
Асп. Плиева Л.Ю.
Кафедра математического анализа.
Северо-Осетинский государственный университет
Статья
посвящена одному квадратурному процессу, построенному Д.Г. Саникидзе в 
.
В приближенных вычислениях особое место занимают квадратурные формулы с наивысшей степенью точности. Их преимущество перед другими обычными квадратурными формулами заключается в том, что в них применяется минимальное количество узлов, коэффициентов и результаты получаются с наименьшей погрешностью. Квадратурные формулы указанного типа были построены еще в XIX в. Гауссом. Поэтому такие квадратурные формулы получили название квадратурных формул Гаусса. В дальнейшем в развитие этой теории значительный вклад внесли А.Крылов и В.Крылов [1].
Здесь
же мы рассмотрим квадратурную формулу, которая была построена в
, (1)
где
– весовая функция и 
, а 
– дифференцируемая до определенного порядка
функция.
Итак, квадратурная формула для (1) имеет вид:
,
где
,
, 
,
,
.
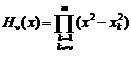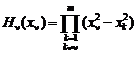Здесь
являются узлами квадратурной формулы, 
, 
– коэффициентами, а 
– остаточным членом.
В
статье Д.Г.Саникидзе [2] приведена таблица узлов и коэффициентов для случая 
, которые не
позволяют вычислить интеграл с более высокой степенью точности из-за отсутствия
дальнейших значений узлов и коэффициентов.
Наша
задача заключалась в том, чтобы построить указанную квадратурную формулу для
конкретных значений .
В
[2] вычисляют из следующей системы нелинейных
уравнений:
(
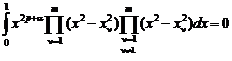). (2)
Используя свойства ортогональности многочленов, можно (2) заменить следующей эквивалентной системой:
. (3)
Отсюда
для любого 
мы будем получать формулы Вьета, т. е. наша
задача свелась к решению обыкновенного алгебраического уравнения -ой степени:
(4)
где
. Для его
решения и вычисления коэффициентов была составлена программа на языке Паскаль
для значений:
.
Ниже
мы приводим полученные результаты для 
и 
:
, 
1,072244199477261880,
0,505492653760114758,
0,421908758347199805,
0,888813304815261389,
0,153346705375644365,
16,705000673599787900,
0,021010252334716897,
1,018984571918536970,
0,103866983666919520,
0,481159060055772372,
0,239874720072333520,
0,304701660614504889,
0,410803984491100701,
0,210697676646705469,
0,593708243717703457,
0,148242465067985048,
0,764030577337008023,
0,100794530327821750,
0,898906161681775344,
0,061185532509305821,
0,980260135888473404,
0,025642390273945643,
15,297184223170844100;
0,011538570831164812,
0,992093361560775528
0,057797996308034946,
0,475206996405231443,
0,136691350037226988,
0,309481687628868688,
0,242410221548385496,
0,224182021687137567,
0,367149993172128210,
0,170025942566687891,
0,501699747781751390,
0,131105212017457282,
0,636123814574765828,
0,100675698014444633,
0,760495808704081177,
0,075350705067579744,
0,865631994733214915,
0,053206548788294829,
0,943770905120913118,
0,033031548416791457,
0,989161252517134264,
0,014001581712479520,
14,843217392368502800.
Замечание.
При проверке достоверности полученных результатов на многочисленных примерах
оказалось, что при 
погрешность округления значительно влияет на
точность результатов. Следовательно, желательно использовать полученные
результаты при 
.
Список литературы
1. Крылов В. И. Приближенное вычисление интегралов. М.: Физ. мат. изд., 1959.
2. Саникидзе Д. Г. О приближенном вычислении некоторых несобственных интегралов // Труды Тбилисского мат. университета, 1965. Т.110.
Для подготовки данной работы были использованы материалы с сайта http://www.skgtu.ru/
Дата добавления: 02.09.2009
