Законы движения планет
Конические сечения
Конические сечения играют в астрономии выдающуюся роль, причем не только в небесной механике, но и оптике, поэтому стоит уделить им особое внимание. Конические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола. Все они является геометрическим местом точек, для которых отношение расстояний их до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету e. При e < 1 получается эллипс, при e = 1 - парабола, при e > 1 - гипербола.
|
|
|
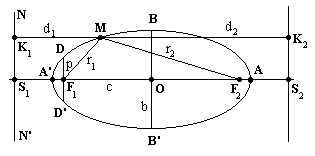
Рис. 1. Эллипс. |
Эллипс изображен на рис. 1. Точки A, A', B, B' - вершины эллипса, O - центр, AA' - большая ось (|OA| = |OA'| = a - большая полуось), BB' - малая ось (|OB| = |OB'| = b - малая полуось), F1 и F2 - фокусы (точки, лежащие на большой оси по обе стороны от центра на расстоянии с = (a2-b2)1/2 от него), e = c/a - эксцентриситет (е < 1), |F1D| = |F1D'| = p = b2/a - фокальный параметр (половина хорды, проведенной через фокус параллельно малой оси). Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2) есть величина постоянная и равная длине большой оси: r1 + r2 = |AA'| = 2a.
Директрисы - прямые, параллельные малой оси, находящиеся на расстоянии |OS1| = |OS2| = d = a/e от нее. Если обозначить расстояния от произвольной точки эллипса М до директрис как |MK1| = d1 и |MK1| = d2 , то для любой точки М эллипса выполняется соотношение r1/d1 = r2/d2 = e.
Предельным случаем эллипса является окружность, которую можно представить как эллипс с фокусами, совпадающими с центром, поэтому для окружности
с = 0,
a = b = r1 = r2 = p,
e = 0
Директрисы для окружности не определены.
|
|
|
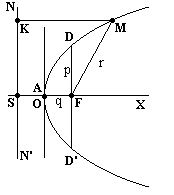
Рис. 2. Парабола. |
Парабола изображена на рис. 2. OX - ось параболы, O - вершина, F - фокус (точка, лежащая на оси на расстоянии p/2 от вершины), NN' - директриса (прямая, перпендикулярная оси и пересекающая ее на расстоянии |OS| = p/2 от вершины по другую сторону от фокуса), p - фокальный параметр (расстояние от фокуса до директрисы или половина хорды DD', проходящей через фокус перпендикулярно оси). Парабола определяется как геометрическое место точек, равноудаленных от данной точки (фокуса) и от данной прямой (директрисы): |MF| = r = |MK|. Поэтому для параболы эксцентриситет e = 1.
|
|
|
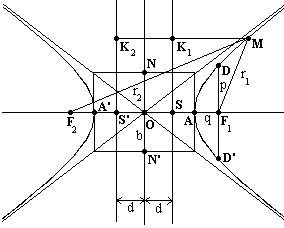
Рис. 3. Гипербола. |
Гипербола изображена на рис. 3. AA' = 2a - действительная ось, A, A' - вершины, О - центр, F1 и F2 - фокусы (точки, лежащие на действительной оси по обе стороны от центра на расстоянии с > a от него), NN' - мнимая ось (|NN'| = 2b = 2*(c2 - a2)), p = b2/a - фокальный параметр (половина хорды, проведенной через фокус перепендикулярно действительной оси). Эксцентриситет e = c/a > 1. Гипербола определяется как геометрическое место точек, для каждой из которых разность расстояний до двух заданных точек (фокусов) есть величина постоянная и равная 2a. Если для произвольной точки М обозначить |MF1| = r1 и |MF2| = r2, то точки, для которых r1 - r2 = 2a, лежат на одной ветви гиперболы (на рис. 3 - левой), а для которых r2 - r1 = 2a - на другой ветви (правой).
Директрисы - прямые, перпендикулярные к действительной оси и расположенные на расстоянии d = a/e от центра. Для любой точки М гиперболы выполняется соотношение r1/d1 = r2/d2 = e, где d1 = |MK1| и d2 = |MK2|.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://colonization.narod.ru/
Дата добавления: 05.06.2008