Элементы квантовой механики

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ.

В настоящее время развитие вычислительной техники проходит, в основном, в двух направлениях:

1. развитие и усовершенствование схематических решений средств ВТ

2. усовершенствование архитектурных решений ВТ

Одним из основных показателей качества средств ВТ является производительность (быстродействие) вычислительной системы. Необходимо отметить, что основной резерв повышения производительности в настоящее время следует искать в развитии второго направления, однако, это нисколько не означает, что первое направление, как утверждают некоторые авторы, себя исчерпало.

Развитие компьютерной электроники неразрывно связано (определяется) с достижениями в области микроэлектроники. Основными элементами ЭВМ являются разнообразные интегральные схемы (ИС), представляющие собой набор электрически связанных между собой активных (полупроводниковые структуры) и пассивных (резисторы, конденсаторы) компонентов, которые выполняют определённые функции.

Основным компонентом ИС являются полупроводниковые приборы, параметры которых в основном определяют параметры ИС и, следовательно, при одинаковых архитектурных решениях ЭВМ и её параметры (в том числе и производительность).

Физические процессы, протекающие в полупроводниковых приборах невозможно объяснить не прибегая к основным положениям квантовой механики и физики твёрдого тела. Из курса физики известна двойственная природа света (волновая и корпускулярная).

В 1924г. физик де-Бройль высказал гипотезу, которая затем была подтверждена экспериментально, согласно которой такими же свойствами должны обладать и микрочастицы (электроны, протоны, атомы и т.д.). Соотношение де-Бройля:

hn=E

l=h/mJ, где

-34

h – постоянная Планка; = 0,6*10 Дж ×с

E – энергия частицы

n - частота излучения

m – масса частицы

J - скорость частицы

Так как микрочастицы (в частности электроны) обладают свойствами корпускулы и волны, то описывать их движение методом классической механики невозможно. Уравнение, описывающее их движение, было найдено Шредингером и носит его имя:

2 2 2 2 2 2 2

iђdy/ dt = ђ/2m( dy/dx + dy/dy +dy/dz ) – U(x,y,z,y) где

ђ = h/2p

y(x,y,z,t) – так называемая волновая функция – решение уравнения

U – потенциальная энергия частицы

В общем случае решение уравнения Шредингера встречает затруднения. Для практических задач уравнение часто существенно упрощается (например, y не является функцией времени; для других задач достаточно рассматривать движение только по одной координате и т.д.).

Решая приведённое уравнение с различными ограничениями (частные случаи), можно получить фундаментальные положения, объясняющие многие процессы в твёрдом теле (физика твёрдого тела). Например, таким образом, удалось объяснить явление туннельного эффекта – преодоление частицей, имеющей энергию E потенциального барьера высотой U и конечной толщины d, даже тогда, когда U>E. Причём, легко доказывается, что при этом микрочастица, просочившаяся (туннелируемая) через барьер, сохраняет свою прежнюю энергию Е.

Как мы увидим позже, явление туннельного эффекта довольно широко используется в схемотехнике ЭВМ.

ПОЛУПРОВОДНИКИ.

В природе все вещества обладают способностью в той или иной степени проводить электрический ток. Это свойство характеризуется значением идеальной проводимости s.

-10 -9 -4 -3

0 10 10 10 10 s

Идеальный Диэлект- Полупроводники Полупроводники s = ¥

диэлектрик рик Идеальный

проводник

Такое деление весьма условное, особенно между ПП и диэлектриками (принципиальных различий нет). Что касается различий между металлами и полупроводниками, то различия здесь более принципиальные.

В настоящее время, наиболее широкое применение в интегральной технологии получил ПП – кремний. Поэтому, в дальнейшем, все примеры, кроме особо оговоренных, основаны на свойствах кремния.

Подавляющее большинство полупроводников (за исключением т.н. аморфных ПП) имеют ярко выраженную кристаллическую структуру и представляют собой в основном монокристаллы. Так простейшая кристаллическая решётка Si – куб. В вершинах куба (для тетраэдра и в центрах граней) находятся атомы Si. Известно, что Si – 4-х валентный т.е. 4 электрона внешней оболочки отсутствуют. Такой уровень является энергетически неустойчивым и атом Si пытается захватить 4 недостающие е с рядом находящихся аналогичных атомов, в свою очередь заимствуя им свои внешние е. При этом возникают специфичные обменные силы, обусловленные по парным объединением валентных е соседних атомов. Такая связь называется ковалентной (или просто валентной).

-- --

а)

b) -- --

Т.к. структура кристалла регулярна, то это приводит к анизотропии - зависимости свойств от направления. Ориентация кристалла задаётся с помощью кристаллографических осей и перпендикулярных им кристаллографических плоскостей. Эти оси и плоскости обозначаются трёхзначными индексами Миллера ( оси [], плоскости () ).

Z (110)

3| 2 [101]

4 1 (100)

(111)

8 7 X [100]

5 6 [111]

Y a) b) c)

Каждой кристаллографической плоскости соответствует различная плотность _________ атомов, поэтому и различие в свойствах.

1,4 2,3 4 3 2 4 1,3 2

1,8

5,6 7,8 5 7 5 6,8 7

а) b) c)

НОСИТЕЛИ ЗАРЯДА В ПП.

Электропроводность вещества объясняется наличием свободных носителей заряда, которые могут перемещаться в объёме вещества, либо под воздействием поля, либо при наличии градиента их концентрации в веществе (стремление к выравниванию концентрации).

Как же образуются свободные носители заряда в ПП?

Идеальный ПП при Т = абсолютному нулю (ПП не имеет дефектов кристалла, поэтому валентные е всех атомов участвуют в ковалентных связях, т.е. они не свободные) является идеальным диэлектриком. При повышении Т°(*) электроны приобретают дополнительную энергию и в конечном итоге некоторые ковалентные связи разрываются, образуя свободные е и незаполненную связь – «дырку» вблизи атома с недостающим е (образуется электронная дырочная пара). Такой процесс называется термогенерацией. Отсутствие е недолговечно (время жизни), на его место приходит е из соседних атомов (рекомбинация), т.е. «дырка» дрейфует. Такая проводимость ПП называется собственной проводимостью, а ПП – собственным ПП (особенность – количество е всегда равно количеству «дыр»).

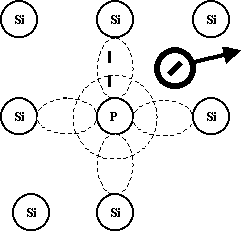
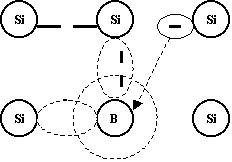
Интересные явления наблюдаются при замещении некоторых атомов Si так называемыми примесными (примесь замещения, есть ещё и примесь внедрения) атомами другой валентности (3 и 5) (копр. 5 вал. Р или 3 вал. бор, Аl).

a) b)

В первом случае 9 е атома фосфора легко «отрывается» от него образуя ион +, а е добавляется к собственным свободным е и равновесие – «дырка» нарушается. Проводимость становится преимущественно е – нной (n – проводимость).

Во втором случае все 3 е бора связаны с соседними атомами Si, образуя «дырку», а атом примеси превращается в неподвижный ион -. ПП приобретает дырочную (Р) проводимость. Такие проводимости называются примесными проводимостями. Носители, находящиеся в большинстве, называются основными, другого типа не основными.

ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВ

е отдельно взятого атома зависит от того, на какой оболочке он находятся, имеют строго одиночное значение энергии. Под влиянием межатомных сил в кристалле эти энергетические уровни расширяются и превращаются в энергетическую зону (Эффект Штарка). Нас будет интересовать энергетическая зона внешней оболочки (т.н. валентная зона). Для того, чтобы е покинул валентную зону и стал свободным, обеспечивающим проводимость, ему необходимо сообщить определённую дополнительную энергию, после чего он попадает в так называемую зону проводимости.

Величина дополнительного энергетического импульса различна для различных полупроводников и определяет ширину так называемой запрещённой зоны. Собственно, ширина запрещённой зоны, а, следовательно, и вид зонной диаграммы, и отличает ПП от диэлектрика.

W(энергия)

j Зона проводимости

Зона проводимости

донорная(n)

примесь Запрещённая зона

Запрещённая зона {

акцент.(р)

Валентная зона примесь Валентная зона

ПП Диэлектрик

Таким образом, ширина запрещённой зоны определяет энергию, необходимую для перехода е из валентной зоны в зону проводимости, и является важнейшим параметром ПП. Если е возвращается в валентную зону, то происходит рекомбинация е и дырки.

В электронике оценка энергии е производится величиной

W = gj, где

j - потенциалов, прошедших элементарным зарядом (иногда, энергетическим потенциалом).

В зависимости от количества атомов примеси и от энергии, получаемой е внешних оболочек (в частности от Т° ПП) количество е зоны проводимости будет различно. Но ведь количество носителей тока при наличии поля будет определять, в частности, величину тока в ПП. Поэтому количество таких е («дырок») является важным параметром. Однако, само количество е («дырок») ещё ни о чём не говорит. Важна их концентрация (т.е. количество на единицу объёма).

Концентрация носителей (обозначается n – для е и p – для «дырок») – очень важный параметр ПП. Концентрация сильно зависит от Т° (например, увеличение Т на 5% увеличивает концентрацию на ~ 3 раза) и от ширины запрещённой зоны (обратно пропорционально). В ПП концентрация носителей неравномерна ( т.е. существует градиент концентрации). Такое неравномерное распределение носителей называется Больумановским равновесием и объясняется возникновением внутреннего электрического поля в ПП, препятствующего выравниванию концентрации.

Движение носителей в электрическом поле напряжённостью Е называется дрейфом и величина дрейфового тока:

i = sE, где

s - удельная проводимость, важный параметр ПП (иногда используют удельное электросопротивление r = 1/s).

Т.к. в ПП есть 2 типа носителей, то

s = qnmn + qpmp,где

q – единичный заряд

n и p – концентрация

mn и mp – подвижность носителей, важный параметр ПП.

В вакууме носитель под воздействием поля Е будет двигаться равноускоренно. Другое дело – твёрдое тело. Ускоряясь, носители постоянно «сталкиваются» с атомами (испытывают рассеяние). На длине свободного пробега носители двигаются равноускоренно, затем, столкнувшись, теряют скорость и снова ускоряются. Поэтому средняя дрейфовая скорость _

J = mЕ, где

m - коэффициент пропорциональности, называемый подвижностью носителя, и зависящий от его эффективной массы (для Si me ~ 3mp).

Быстродействие полупроводниковых приборов прямо пропорционально подвижности носителей ПП, на основе которого выполнен прибор.

Подвижность – величина не постоянная и зависит от Т°, причём неоднозначно, например

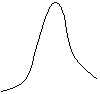
m Так, для Si m могут меняться в диапазоне рабочих температур

от -50°С до +125°С в 4-5 раз.

ЭФФЕКТ ПОЛЯ

Эффект поля – это изменение концентрации носителей (а, следовательно, проводимости) в приповерхностном слое ПП под воздействием внешнего электрического поля.

Создадим конструкцию МДП:

+ d ++ +++

· · Т.к. есть диэлектрик, то ток не течёт. Из-за свойств

Me Eд диэл. -- U + проводника все свободные е сосредоточены на

поверхности проводника. На обкладке, представляющей

собой ПП будет наведён такой же заряд, что и в провод

нике, однако, он будет распределён неравномерно в глубь

кристалла.

Поле в диэлектрике, ввиду отсутствия объёмных

X зарядов, постоянно. В ПП р-типа, при подаче +U

на ПП, на границе ПП – диэлектрик концентрация

U изменений р – типа увеличивается, следовательно,

увеличивается и проводимость. Увеличение концентрации оситных носителей в слое называется обогащением (уменьшение – объединением при неизменной полярности U ). По мере уменьшения d эффект поля может исчезнуть за счёт пробоя диэлектрика. Даже если диэлектрик – вакуум, возможен туннельный эффект.

Глубина проникновения поля в ПП (фактически, толщина обогащённого слоя) называется длиной Дебая (дебаевская длина).

ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ

В подавляющем большинстве случаев в микроэлектронике находят применение так называемые p-n переходы, возникающие на границе металл – полупроводник и полупроводник – полупроводник. Комбинация двух ПП различной проводимости обладают вентильными свойствами, т.е. они лучше пропускают поток в одном (прямом) направлении. Практически все реальные p-n переходы - плавные, т.е. в районе металли

p-n переход ческой границы концентрация одних примесей

p n

постоянно растёт, а других – убывает. Сама металли

ческая граница характеризуется равенством p=n.

Как правило, концентрация p и n вне границы

металлическая граница существенно различаются, и такие p-n переходы

называются асимметричными (несимметричными).

Т.к концентрация n > p, то число электронов, диффундирующих в область р больше, чем число диффундирующих «дырок» и в слое р вблизи границы оказываются избыточные е, ре-комбинирующие с «дырками» до тех пор, пока не будет равновесия. Следовательно, концентрация «дырок» уменьшится. Аналогично можно рассуждать и по отношению к «дыркам».

Например:

асимметрия

n n,p

идеальный

переход

В идеале считают, что в p-n переходе Ширина перехода (d)

вообще отсутствуют носители и сам p-n переход является наиболее высокоомной частью структуры. Т.к. концентрация p и n различна, то между p и n областями, разделёнными высокоомным переходом, возникает потенциальный барьер. Если к переходу приложить напряжение + и к p-области (такая полярность называется прямой), то высота потенциального барьера уменьшится и

Поиск по рефератам и авторским статьям

Элементы квантовой механики

ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВ

ЭФФЕКТ ПОЛЯ

U изменений р – типа увеличивается, следовательно,

Глубина проникновения поля в ПП (фактически, толщина обогащённого слоя) называется длиной Дебая (дебаевская длина).

ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ

КРАТКАЯ ХАРАКТЕРИСТИКА РАЗЛИЧНЫХ ТИПОВ ПП ДИОДОВ

n+ n

РЕЖИМИ РАБОТЫ ТРАНЗИСТОРА

СИСТЕМЫ ПАРАМЕТРОВ ТРАНЗИСТОРОВ

i2 = h21i1 + h22J2, где

I1 = ¦(Uбэ)

I1 = I`эо(e (Uбэ/jт) - 1) (2)

К +/- = Iвых/Iвх = Iк/ Iэ » h21б < 1

S = Iб/Iбн, где

S £ 1 – соответствует линейному активному режиму

МДП ТРАНЗИСТОР С ИНДУЦИРОВАННЫМ КАНАЛОМ

МДП ТРАНЗИСТОРЫ СО ВСТРОЕННЫМ КАНАЛОМ

СХЕМЫ ВКЛЮЧЕНИЯ МДП ТРАНЗИСТОРОВ