Теорема Стюарта
Проектная работа по математике
Выполнила: Сосунова Татьяна, 10 класс
Руководитель: Галошина В. И.
МОУ Яркульская СОШ
2010 год
Введение:
У меня есть некоторые проблемы в умении доказывать
теоремы и выводить формулы. Поэтому я с удовольствием приняла предложение моего
учителя по математике изучить теорему Стюарта. Во всех источниках была дана
только формулировка теоремы и формула, а так же в справочниках есть формулы для
вычисления медианы и биссектрисы треугольника. Доказывать и выводить формулы
мне пришлось самостоятельно. Теорема Стюарта названа по имени доказавшего её
английского математика М. Стюарта и опубликовавшего её в труде «Некоторые общие
теоремы» (1746, Эдинбург). Теорему сообщил Стюарту его учитель Р. Симсон,
который опубликовал эту теорему лишь в
Цели:
Расширить круг изучаемых в школе теорем
Научиться применять теорему для решения задач
Задачи:
Изучить и доказать теорему Стюарта
Получить формулы для вычисления длин медиан и биссектрис треугольника
Рассмотреть применение теоремы Стюарта для решения задач на нахождение длин замечательных линий треугольника
Теорема Стюарта
Произведение квадрата расстояния от точки, лежащей на стороне треугольника, до противоположной вершины на длину этой стороны равно сумме квадратов оставшихся сторон на несмежные с ними отрезки первой стороны без произведения этих отрезков на длину основания.
AD2*BC = AB2*CD + AC2*BD – BC*BD*CD
Дано:
ABC
DЄBC
Доказать:
AD2*BC = AB2*CD + +AC2*BD – BC*BD*CD
Доказательство:
A
|
c |
|
b |
|
ac |
|
ab |
|
a |
|
D |
B C
Для доказательства используем теорему косинусов:
a2= b2+c2 – 2bc cosA (Квадрат стороны треугольника равен сумме квадратов других его сторон минус удвоенное произведение этих сторон на косинус угла между ними)
2bccosA=b2+c2 - a2
cosA =
Рассмотрим ABC:
cosB= 
Рассмотрим BAD:
cosB=
3. Откуда:
=
Обе части умножим на 2AB:
=
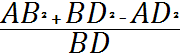
По свойству пропорций:
AB2*BD+BC2*BD-AC2*BD = AB2*BC+BD2*BC-AD2*BC
AD2*BC= - AB2*BD-BC2*BD+AC2*BD+AB2*BC+BD2*BC
AD2*BC= AB2 (BC-BD)-BC*BD(BC-BD)+AC2*BD
AD2*BC= AB2*DC-BC*BD*DC+AC2*BD, то есть
AD2*BC = AB2*CD + AC2*BD – BC*BD*CD
Теорема доказана.
Применение теоремы Стюарта для нахождения длин замечательных линий треугольника
Вычисление медианы треугольника:
Дано:
ABC
a, b, c- стороны треугольника
ac , ab - части a
ma- медиана к стороне a
Найти:
ma
|
A |
|
c |
|
b |
|
ma |
|
a |
|
ac |
|
ab |
|
C |
|
D |
|
B |
ma2a=c2ab+b2ac-acaba
ma=
ma=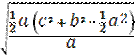
ma=
=
Вычисление биссектрис треугольника:
Дано:
ABC
a, b, c- стороны треугольника
ac , ab - части a
la- биссектриса к стороне a
Найти:
la
|
А |
Решение:
 |
|||||
|
b |
|||||
 |
|
la |
|
C |
|
a |
|
ab |
|
aс |
|
B |
|
c |
la2a=c2ab+b2ac-abaca
la2=
По свойству биссектрис: биссектриса делит противоположную сторону на отрезки пропорциональные прилежащим сторонам:
, откуда
ab=
; ac=
la2=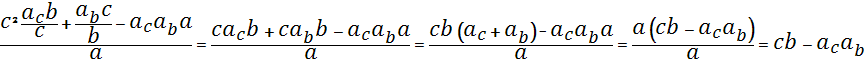 
, то есть la= 
Решение задач
Вычисление биссектрисы треугольника
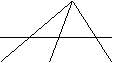
Задача: отрезок AD является биссектрисой треугольника
ABC, AB=14 см, BC=20 см, AC=
Дано:
ABC,
AB=14 см, BC=20 см, AC=
Найти:
AD
|
A |
 |
|
B |
|
C |
|
D |
По свойству биссектрисы: биссектриса делит противоположную сторону на отрезки пропорциональные прилежащим сторонам:
= 
Пусть BD=x
=
21x=14(20-x)
35x=280
x= 8(см), т.е. DC=12 (см)
2) По теореме Стюарта:
AD=
= 
= 3
(см)
Ответ: 3 см
Вычисление медианы треугольника
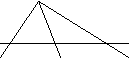
Задача: отрезок AD является медианой треугольника ABC, AB=12см,
BC=16 см, AC=20 см. Найти AD.
Дано:
ABC,
AB=12см, BC=16см, AC=
|
A |
 |
|
C |
|
B |
|
D |
Медиана делит сторону пополам:
BD=DC=8(см)
По теореме Стюарта:
AD =
Ответ: 4
см
Выводы:
Теорема Стюарта расширяет возможности решения задач по нахождению элементов треугольника
Работа была интересной, хотя и трудной в плане вывода формул
Эту теорему и следствия из нее для вычисления длин замечательных линий треугольника необходимо знать каждому выпускнику
Список литературы
Г. И
Глейзер.
История математики в школе. 9-10 класс. Москва «Просвещение». 1983
Приложение «Математика» к газете « 1 сентября»
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Дата добавления: 27.08.2011
