Великая теорема Ферма
Великая теорема Ферма
Валерий Петров
Более 350 лет математики всего мира безуспешно ищут ответ на вопрос: «Верна ли великая теорема Ферма?». Не находит его и дьявол, изучив за 10 часов все без исключения разделы математики и потратив остаток времени на собственные изыскания, он, за 10 минут до истечения срока, появляется с пачкой исписанных листков, швыряет их на пол и топчет ногами. И, признав свое поражение, исчезает... Однако спустя несколько минут появляется вновь и вместе с человеком начинает искать ответ на поставленный вопрос».
В действительности, однако, все было несколько иначе. Когда дьявол узнал об условии заключения договора с ученым-математиком о продажи его души, он рассмеялся и сказал: «Нет ничего проще. У меня есть доказательство этой теоремы, написанное самим Ферма». С этими словами дьявол достал из кармана аккуратно сложенный лист бумаги и протянул его ученому. Флэгг уселся поудобнее в кресло у камина и стал читать.
«Пусть имеется три целых числа, удовлетворяющих уравнению:
|
z3 = x3 + y3 |
(1) |
Очевидно, эти числа попарно не должны иметь общих множителей. Также очевидно, что число z меньше суммы двух других чисел, т.е.
|
z < x + y |
(2) |
Пусть имеется три отрезка длиной z, x, y, удовлетворяющих условию (2). Тогда в силу известной теоремы на этих отрезках можно построить треугольник как на сторонах. Предположим, что треугольник прямоугольный. Тогда для сторон этого треугольника справедливы два соотношения:
z3 = x3 + y3 и z2 = x2 + y2,
откуда следует:
![]()
![]()
(x3 + y3)2 = (x2 + y2)3;
x6 + 2x3y3 + y6 = x6 + 3x4y2 + 3x2y4 + y6;
2x3y3 = 3x4y2 + 3x2y4;
2x3y3 = 3x2y2(x2 + y2);
2xy = 3(x2 + y2).
Пусть x = y + b. Тогда:
2y(y + b) = 3(x2 + y2);
2y2 + 2yb = 3x2 + 3y2;
2y2 + 2yb – 3y2 = 3x2;
2yb – y2 = 3x2;
y(2b – y) = 3x2;
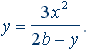
Пусть 2b – y = c, тогда y = 3x2/c.
Пусть 3/c = d, тогда
|
y = dx2 |
(3) |
Таким образом, число x является одним из сомножителей числа y, что недопустимо и, следовательно, уравнение (1) не имеет целочисленных решений удовлетворяющих условию (2).
Применяя бином Ньютона для возведения в степень суммы чисел x2+y2 в степень, можно аналогичным образом доказать теорему для любых чисел n>3.
Известно, однако, что существует теорема, согласно которой треугольник, между сторонами которого имеется соотношение zn=xn+yn, при n>3 является остроугольным. Тогда для сторон этого треугольника справедливы два соотношения:
zn = xn + yn и z2 = x2 + y2 + 2xy · cosα,
где α – угол между сторонами x и y.
Однако и в этом случае доказательство сводится к тому, что y оказывается равным dx2, так же, как это было показано для прямоугольного треугольника (3).
Флэгг задумался на мгновенье и неожиданно швырнул бумагу прямо в огонь. «Зачем Вы это сделали?» – воскликнул дьявол. «Я нахожу, что слишком дешево продал свою душу. Так пусть же никто больше не воспользуется этим доказательством!» – ответил Флэгг.
«В самом деле», подумал дьявол, «пусть математики еще поломают головы над доказательством этой теоремы».
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.n-t.org/
Дата добавления: 31.10.2004


