Проектирование и разработка сетевых броузеров на основе теоретико-графовых моделей
Выполнил студент 5 курса
специальности «информатика»
_________________Поляков Т.И.
Симферополь
| Содержание | |
| Введение | 2 |
| Глава I. Теоретико-графовые модели организации сетевых структур | 3 |
| 1.1. Основные понятия теории графов | 3 |
| 1.2. Графовые алгоритмы | 5 |
| Глава II. Сетевые структуры на базе теоретико-графовых моделей | 11 |
| 2.1. Методы построения сетевых структур | 11 |
| 2.2. Классификация существующих методов организации сетей | 12 |
| 2.3. Глобальная сеть Internet | 16 |
| 2.4. Основы сетевой маршрутизации | 20 |
| 2.5. Алгоритмы маршрутизации | 24 |
| Глава III. Сетевые броузеры | 33 |
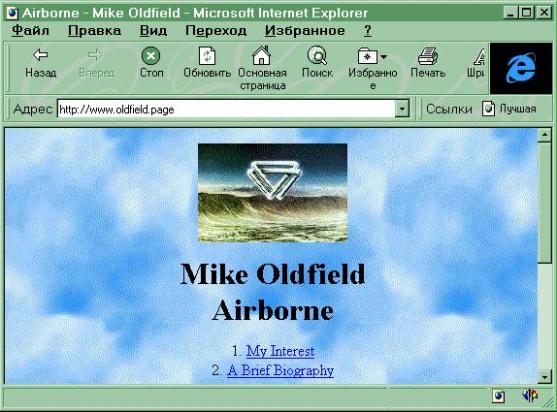
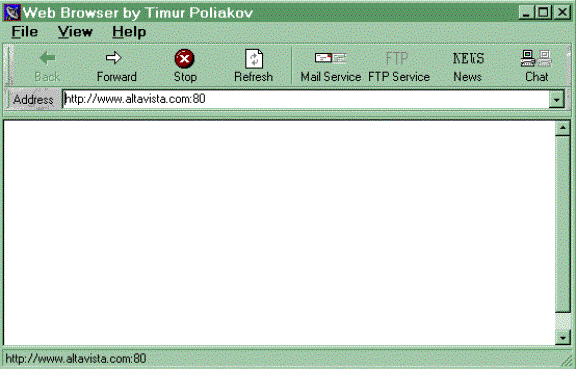
| 3.1. Описание стандартного броузера | 33 |
| 3.2. Характеристика существующих систем поиска | 33 |
| 3.3. Особенности создания броузеров в визуальных средах программирования | 40 |
| Глава IÑ. Программная реализация | 44 |
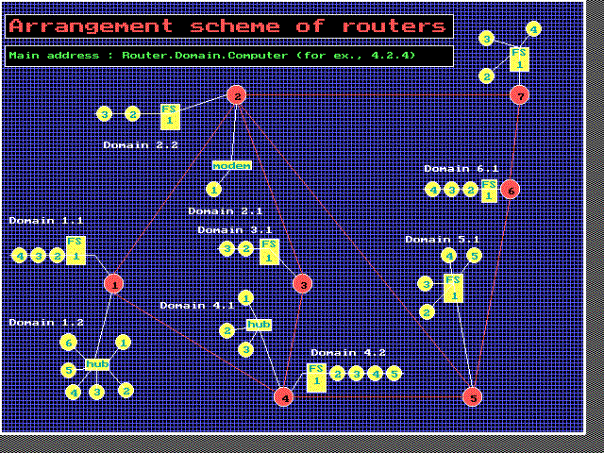
| 4.1. Архитектура системы “броузер” | 44 |
| 4.2. Основные процедуры броузера | 45 |
| 4.3. Архитектура имитационной модели глобальной сети | 47 |
| 4.4. Основные процедуры имитационной модели | 48 |
| Заключение | 50 |
| Список литературы | 51 |
| Приложение 1 – исходный текст программы “броузер” | 52 |
| Приложение 2 – исходный текст модели корпоративной сети | 91 |
Введение
Актуальность
В связи с расширением глобальной сети Internet возрастает необходимость внедрения новых оптимизационных алгоритмов, связанных со скоростью обмена данных между компьютерами в единой сети. Компьютерные сети завоевывают мир. Системы из маленьких компьютеров превращаются в огромные хранилища данных, доступные всему миру. Любая современная фирма, любой офис оснащен хотя бы простейшей сетью. Не выходя из дома, сотни тысяч людей работают на персональных компьютерах, принося пользу всему миру. В основном для работы в Internet используются программы-броузеры. Эти программы позволяют легко обмениваться текстовой, графической и звуковой информацией, используя популярную, простую в обращении мультемедийную службу ИНТЕРНЕТ World Wide Web.
Цель
Цель данной работы заключается в следующем :
- разработка математической модели сетевого броузера и корпоративной среды;
- создание имитационной модели распределении информации в глобальных сетях.
Для достижения данной цели были решены следующие задачи:
1.) Проведен анализ существующих броузеров;
2.) Рассмотрены основные топологии существующих корпоративных сетей;
3.) Разработан алгоритм определения оптимального маршрута передачи
информации по глобальной сети.
1.Теоретико – графовые модели
организации сетевых структур
1.1. Основные понятия теории графов
Определение. Множество Х=
и набор U неупорядоченных пар объектов (
) из Х называется графом Г. Объекты множества Х называются
вершинами графа, а наборы объекта U – ребрами графа. Про ребра 
будем говорить, что они соединяют вершины 
и 
.
В случае, если множество Х и набор U состоят из конечного числа объектов и пар, то граф Г
называется конечным.
Пусть 
и 
- произвольные вершины графа Г.
Определение. Система ребер графа Г 
называется путем, соединяющим вершины 
и 
.
Определение.Путь 
, не проходящий дважды одно ребро, называется циклом,
если 
=
. В частности, цикл 
будем называть петлей.
Определение. Граф Г называется связным, если для любых двух различных
вершин 
и 
графа Г существует путь, соединяющий эти вершины.
 |  | ||||
 | |||||
 |  |  |
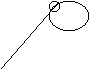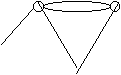Рис. 1
Легко видеть, что граф из примера 1 является конечным, несвязным и содержащим петли.
Определение. графы Г и Г` называются изоморфными, если существует взаимно однозначное соответствие между их вершинами и ребрами такое, что соответствующие ребра соединяют соответствующие вершины.
Определение. Граф Г` называется подграфом Г, если его вершины и ребра принадлежат графу Г.
Длиной пути в графе называют сумму длин входящих в этот путь ребер.
Определение. Деревом называется конечный связный граф с выделенной вершиной, именуемой корнем, не содержащий циклов.
 |
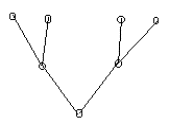Если в графе можно выделить более одного дерева, которые не связны между собой, то такой граф называют лесом.
Рис 2. Лес, имеющий две компоненты связности (2 дерева).
Будем далее обозначать через Х – множество вершин и U – множество ребер графа, а сам граф, определяемый этой парой объектов, будем обозначать <X,U>;
x ÎX, u ÎU. Обозначим длину дуги u=(x,y) через d(u). Кратчайшую длину пути из х в
z обозначим D(x,z).
Очевидно, если кратчайший путь из x в z существует и проходит через промежуточную вершину w, то D(x,z) = D(x,w) + D(w,z). Эта формула справедлива для любой промежуточной вершины w рассматриваемого пути, в том числе и для последней, смежной с конечной вершиной w. Поэтому кратчайший путь можно отыскать, последовательно переходя от конечной вершины z в ближайшую смежную и запоминая цепочку построенных вершин (конечно, при условии, что хотя бы один путь между вершинами x и z существует и граф не содержит циклов. Эта идея и является в сущности принципом Р.Беллмана.
1.2. Графовые алгоритмы
Алгоритм Беллмана поиска кратчайшего пути между двумя вершинами связного графа, не имеющего циклов с неотрицательными длинами ребер. Его описание приводится ниже при помощи алгоритмической схемы.
Идентификаторы :
D[w] – рабочий массив, при вычислениях интерпретируется как кратчайшая длина из вершины w в вершину z.
wÎX.
d[s,t] – массив длин ребер графа для каждой пары вершин s,t ÎX. Если некоторое ребро отсутствует, то в элементе этого массива полагается записанным некоторое достаточно большое число, превышающее сумму длин всех ребер графа.
Stack – последовательность вершин, определяющая кратчайший путь из x в z.
Begin
Stack:=’’; // Очистить Stack.
Stack <=z; // Поместить в стек конечную вершину z.
w:=z; // Запомнить первую пройденную вершину.
D[z]:=0; // Обнуление длины пути из вершины z в нее же.
While w=/=x do // Пока не будет достигнута начальная вершина, выполнять
// перебор вершин графа
p:= вершина, для которой величина D[p] = d[p,w]+D[w] минимальна. Если таких вершин несколько и среди них имеется вершина x, то p:=x, если же среди них нет вершины x – взять любую из доставляющих минимум сумме.
Stack <=p; // Записать выбранную вершину в стек.
w:=p; // и взять ее для построения следующего шага.
End;
End.
Пусть число вершин графа |X|=n, а число ребер |U|=m. Оценим сложность этого алгоритма как число шагов выполнения алгоритмической схемы, считая одним шагом выполнение ровно одного выполнимого оператора, каковые представлены только строками 2,3,4,5,6,8,9. В худшем случае выбор вершины в строке 8 (по минимуму расстояния) произойдет в результате просмотра всех n вершин, а цикл с заголовком в строке 6 повторится для всех вершин, поэтому сложность алгоритма можно оценить как C*n^2, где С – некоторая константа, учитывающая реализацию алгоритма в произвольной вычислительной среде.
Следующий алгоритм обеспечивает нахождение кратчайших расстояний от фиксированной вершины х, называемой источником, до всех остальных вершин графа с ограничением, предполагающим отсутствие в графе контуров отрицательной длины (сумма длин ребер, входящих в любой контур, неотрицательна).
Алгоритм Форда-Беллмана
Идентификаторы : d[s,t] – массив длин ребер графа для каждой пары вершин s,t ÎX. Если ребра нет, то соответствующий элемент этого массива содержит достаточно большое число.
х – вершина-источник графа <X,U>.
n=|X| - число вершин графа.
u,w,k – рабочие переменные.
D[w] – массив, в котором к концу работы алгоритма будут содержаться кратчайшие длины путей из х в w для всех вершин w ÎX.
Begin
D[x]:=0; // Длина пути из источника x.
For w ÎX do D[w]:=d[x,w]; // Инициализация матрицы расстояний
For k:=1 to n-2 do // Повторять n-2 раз
For w Î{X\{x}} do // Цикл по всем вершинам, кроме источника.
For u ÎX do D[w]:=min(D[w],D[u]+d[u,w]); // выбор минимума.
End.
Этот алгоритм также основан на соотношении (принципе оптимальности) Беллмана. Всякий раз, когда находится путь через транзитную вершину u, который короче найденного пути из х в w, он заменяется на более короткий путь. Это соотношение должно проверяться для любой возможной из n-2 транзитных вершин при оценке пути в каждую вершину, поэтому в алгоритме имеется цикл, определенный в строке 4.
Алгоритм Дейкстры нахождения кратчайших расстояний от источника до всех остальных вершин применим только тогда, когда граф не имеет контуров или когда веса всех ребер неотрицательны.
Идентификаторы :
d[s,t] – массив длин ребер графа для каждой пары вершин
s,t ÎX. Если ребра нет, то соответствующий элемент этого массива содержит достаточно большое число.
х – вершина-источник графа <X,U>.
n=|X| - число вершин графа.
u,w – рабочие переменные.
D[w] – массив, в котором к концу работы алгоритма будут содержаться кратчайшие
длины путей из x в w для всех вершин w ÎX.
BEGIN
D[x]:=0;
For w ÎX do D[w]:=d[x,w];
T:={X\{x}};
 |
While T=\= do
Begin
w:=вершина r из T такая, что D[r]=min{D[p]:p из T};
T:={T\{w}};
For u ÎT do D[w]:=min[D[w],D[u]+d[u,w]];
End
END
Алгоритм Форда-Фалкерсона нахождения максимального потока в сети.
Многие задачи исследования операций сводятся к анализу потоков, маршрутов, последовательностей событий, протекающих со времени, и других процессов, которые можно представить в виде множества взаимосвязанных элементов. Для математического представления таких процессов удобно их задание в виде графов.
Рассмотрим конечный ориентированный граф Г=(X,u), в котором Х={x1,...,xn}-множество вершин, U – множество дуг.
Пусть x ÎX. Обозначим E+(x) – множество дуг графа, входящих в х, E-(x) – выходящих из х.
Множества начальных вершин дуг из Е+(х) и множество конечных вершин дуг из Е-(х) обозначим соответственно S+(x) и S-(x).
 | |||||
 | |||||
 | |||||
E+(x) E-(x)
 |
 |
y x y
S+(x) S-(x)
Рис. 3. Окрестность вершины графа.
Граф Г называют транспортной
сетью, если каждой дуге u соответствует целое число c(u)>=0 и найдутся x0 и z из Х такие, что Е+(х0)=
Е-(z)= . Вершина х0 называется истоком, z-стоком, c(u) – пропускной способностью дуги. Потоком в транспортной сети называют целочисленную функцию ф(u), удовлетворяющую следующим условиям :
1) 0<=ф(u)<=с(u)
2) ф(u) - ф(u)
= 0 для любой вершины x=/=x0, x=/=z.
u ÎЕ+(х) u ÎЕ-(х)
При этом поток не может «накапливаться» ни в одной вершине транспортной сети, кроме истока х0 и стока z, поэтому
ф(u) = ф(u) = Ф.
u ÎЕ+(х) u ÎЕ-(х)
Величину Ф называют потоком транспортной сети. Дуга u называется насыщенной, если ф(u)=c(u). Поток Ф называется полным, если каждый путь из х0 в z содержит хотя бы одну насыщенную дугу.
Рассмотрим разбиение R множества вершин сети Х = Х1UX2,
X1ÇX2, X1ÇX2=Æ, x0ÎX1, zÎX2, называемое разрезом сети.
Сумма пропускных способностей множества {(xi,xj), xi из X1, Xj из
Х2} определяет пропускную способность разреза R : r(R) = c(u),
uÎ{(xi,xj):xi ÎX1, xjÎX2}
Поскольку для любой дуги u выполняется неравенство ф(u)<=c(u), то Ф<=r(R).
Теорема Форда-Фалкерсона : максимальный поток в сети равен минимальной величине разрезов в этой сети.
Алгоритм нахождения максимального потока, предложенный Фордом и Фалкерсоном, состоит в постепенном увеличении допустимого потока Ф до максимальной величины Ф*. Начальное значение потоков полагается равным нулю. Процесс увеличения потока состоит в поиске путей, на которых возможно увеличение потока, с соответствующей разметкой вершин сети.
Алгоритм Форда-Фалкерсона
Предполагается, что путь из истока в сток с ненулевыми пропускными способностями входящих в него дуг существует.
I. Увеличение потока.
1. Присвоить истоку х0 пометку (+х0, d(x0) = ). Это означает, что вход в исток не ограничен; величина d всегда показывает, на сколько может быть увеличен
поток, входящий в помеченную вершину. Здесь символ обозначает достаточно большое число – начальное
значение пометки.
2. Взять некоторую вершину xi с пометкой, которая в общем случае имеет вид (+ или – xk, d(xi)), где xk – обозначение вершины, d(xi) – некоторое число. Каждой непомеченной вершине xj из S-(xi), для которой ф(xi,xj)<с(xi,xj), присвоить пометку (+xi, min[d(xi),c(xi,xj)-ф(xi,xj)]). Это означает, что поток в дуге (xi,xj) может быть увеличен (знак плюс) на величину, определяемую минимумом. Каждой непомеченной вершине xj из S+(xi), такой, что ф(xj,xi)>0 присвоить пометку (-xi, min[d(xi), ф(xj,xi)]), что означает возможность уменьшения потока на величину, определяемую минимумом.
3. Если сток не помечен и можно пометить какую-либо вершину, кроме стока, то перейти к п.2.
4. Если оказался помеченным сток z, и в его пометку входит число d(z), то между вершинами x0 и z найдется цепь, все вершины которой помечены номерами предыдущих вершин. Для каждой помеченной вершины х в этой цепи изменить величину потока : ф'(y,x)=ф(y,x)+d(z), если х имеет пометку (+y,d(x)) или ф'(y,x)=ф(y,x)-d(z), если х имеет пометку (-y,d(x)). Пометка вершины х стирается, назначенные потоки запоминаются. При достижении (в процессе стирания пометок вершин цепи) истока х0 перейти к п.1; если же ни одну вершину пометить не удается и сток z не помечен, то перейти к построению разреза.
II.Построение разреза.
Искомый минимальный размер R определяется двумя множествами Х1 и Х2, где Х1 – все помеченные вершины, Х2 – вершины, которые не удается пометить. При этом полный поток Ф=Ф* должен быть равен величине полученного минимального разреза.
2.Сетевые структуры на базе
теоретико-графовых моделей
2.1. Методы построения сетевых структур
Компьютерная сеть состоит из элементов, среди которых выделяют компьютеры, предоставляющие ресурсы в сети (серверы), компьютеры, обеспечивающие доступ к сетевым ресурса серверов (клиенты), среду (media), в которой реализованы соединения, и сами ресурсы – файлы, процессоры, принтеры, и другие элементы. В сетях реализуется принципиальная возможность совместного использования и устройств, и данных.
Соединения компьютеров в сети может осуществляться по-разному, и различным типовым способам присвоены различные наименования.
Различают сети с выделенными серверами и одноранговые сети. В настоящее время наиболее распространенными являются сети с архитектурой клиент-сервер, которые используют центральный сервер для обслуживания запросов клиентов, в то время как одноранговые сети позволяют любой рабочей станции функционировать одновременно в качестве сервера, если этого требуют задачи.
В сетях с архитектурой клиент-сервер специализированный компьютер (выделенный сервер) используется для установки всех разделяемых ресурсов. Такое решение ускоряет доступ пользователей к централизованным ресурсам сети и связано с рядом особенностей :
- сетевое администрирование проще за счет незначительного числа серверов в сети и их узкой специализации;
- предъявляются высокие требования к выделенному серверу : для обеспечения высокой производительности требуется установка на сервере большого количества оперативной памяти, диска большой емкости и использования в сервере производительного процессора;
- при нарушении работы сервера сеть становится практически неработоспособной.
Если в одноранговой сети нет выделенного сервера, все компьютеры равноправны в том смысле, что могут рассматриваться и как серверы, и как клиенты. Обычно одноранговые сети содержат до десяти компьютеров.
Одноранговая сеть на основе сервера содержит выделенный сервер. Сеть может содержать не один, а несколько серверов, имеющих специальное назначение :
- файл-серверы;
- принт-серверы;
- серверы приложений, на которых выполняются прикладные задачи;
- почтовые серверы;
- факс-серверы;
- коммуникационные серверы, управляющие потоком данных и почтовых сообщений между сетью, в которой они размещены, и другими сетями, мэйнфреймами (большими ЭВМ) или удаленными пользователями через модемы и телефонные линии;
- серверы служб каталогов, обеспечивающие поиск, хранение и защиту информации в сети.
В комбинированных сетях совмещаются лучшие качества одноранговых сетей и сетей на основе сервера. Используется сервер, но и другие отдельные компоненты могут разрешать доступ к своим данным.
2.2. Классификация существующих методов организации сетей
Базовые топологии локальных сетей
Базовые топологии локальных сетей – это основные виды конфигураций соединений элементов сетей при помощи кабеля.
Рассмотрим три базовых топологии : шина, звезда и кольцо.
Шина (или линейная шина) – это топология, представленная на рис. 4.
 | |||||
 |  | ||||
 |
Рис. 4. Простейшая одноранговая сеть.
Передаваемый сигнал распространяется по кабелю – магистрали (сегменту) и поглощается на концах терминаторами (заглушками). В любой момент времени только один компьютер может вести передачу. Данные передаются всем компьютерам сети, однако информацию принимает только тот, адрес которого соответствует адресу получателя, зашифрованному в передаваемых данных.
Говорят, что шина – пассивная топология. Компьютеры только “слушают”, но не регенерируют сигналы. Подсоединение кабеля осуществляется при помощи баррел-коннекторов и репитеров.
Баррел-коннекторы – это специальные металлические соединительные разъемы; они позволяют сращивать кабель, но при большом количестве стыковок сигнал ощутимо затухает. Для решения проблемы сохранения физических параметров сигналов, распространяющихся в компьютерных сетях, применяют специальные устройства.
Репитер – это повторитель-формирователь, просто усиливающий сигнал.
Топология звезда предусматривает подключение всех компьютеров с помощью сегментов кабеля к центральному элементу. Различают два подтипа этой топологии – пассивная звезда, в центре которой нет компьютера-абонента, кабели соединены при помощи концентратора (hub), и активная звезда, содержащая в центре компьютер, управляющий обменом информации в сети. Концентратором (hub) называют устройство, служащее для объединения нескольких сегментов сети и не преобразующее передаваемую информацию. Сигналы от передающего компьютера поступают через концентратор ко всем остальным. Концентраторы бывают активные, пассивные и гибридные.
Активная звезда обеспечивает бесконфликтное управление, но нарушения в работе центра приводят к выходу из строя всей сети, но зато сеть с такой топологией мало чувствительна к выходу из строя участков соединительного кабеля.
Топология кольцо предусматривает передачу сигналов по кольцу в одном направлении, так, что сигналы проходят через каждый компьютер (рис.5). В отличие от пассивной топологии “шина”, здесь каждый компьютер выступает в роли репитера, усиливая сигналы и передавая их следующему компьютеру.
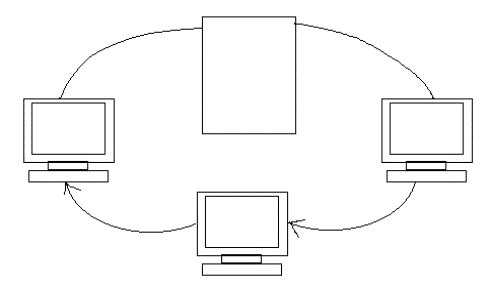
Сервер
Рис.5. Топология “Кольцо”.
Типы кабелей
Тип кабеля, выбранного для соединения сетевых компонентов между собой, определяет максимальную скорость передачи данных в сети и возможную удаленность компьютеров друг от друга. Это связано с частотными свойствами процессов распространения сигналов. Основными и наиболее распространенными являются следующие типы кабелей :
- Коаксиальный (coaxial), подразделяющийся на толстый и тонкий;
- Витая пара (twisted pair), имеющая два типа : неэкранированная (10 Base-T) и экранированная.
- оптоволоконный (fiber optic).
Толстый кабель обеспечивает передачу сигналов на большие расстояния, чем тонкий, -до 500 метров, и часто используется в качестве основного магистрального кабеля (backbone).
Для подключения к толстому коаксиальному кабелю применяют специальное устройство – трансивер (TRANSmitter/reCEIVER – передатчик.приемник), устройство, преобразующее поток параллельных данных, который использует шина компьютера, в поток последовательных данных, направляемых по кабелю к другому компьютеру. Трансивер, используемый для подключения к толстому кабелю, снабжен специальным коннектором, который называют «зуб вампира» или «пронзающий ответвитель». Чтобы подключить трансивер к сетевому адаптеру, нужно подключить кабель трансивера к коннектору AUI- порта сетевой платы. Этот коннектор известен как DB-15 (15-ти контактный).
Витая пара дешевле коаксиального кабеля и менее надежна. Использование неэкранированной витой пары позволяет реализовать длину сегментов соединения до 100 метров. Для подключения витой пары используются восьмиконтактные коннекторы RG-45.
Оптоволоконный кабель имеет высокую стоимость и обладает рядом преимуществ : слабое затухание сигнала, практическая невозможность вскрытия оптоволокна с целью перехвата данных. Такой кабель передает данные только в одном направлении и поэтому состоит из двух волокон с отдельными коннекторами.
Использование оптоволоконного кабеля теоретически может позволить осуществлять передачу данных со скоростью 200000 Мб/сек.
Платы сетевого адаптера
Платы сетевого адаптера принимают параллельные данные с шины компьютера и преобразуют их в последовательный битовый код, используемый при передаче по кабелю. Плата сетевого адаптера должна указать свое местонахождение или сетевой адрес, чтобы ее можно было отличить от остальных плат. Сетевые адреса определены комитетом IEEE, закрепившим за каждым производителем таких плат некоторые интервалы адресов. Эти адреса «зашиты» в микросхемы. Благодаря этому каждая плата и каждый компьютер имеют уникальный адрес в сети. Плата сетевого адаптера запрашивает у компьютера данные из памяти по шине, и если они поступают быстрее, чем может передать плата, то данные временно помещаются в буфер.
Перед передачей данных передающая плата проводит диалог с принимающей платой, осуществляя согласование информации о следующих параметрах передачи :
- максимальном размере блока передаваемых данных;
- объеме данных, передаваемых без подтверждения о получении;
- интервалах между передачами блоков данных;
- интервале, в течение которого необходимо послать подтверждение;
- объеме данных, которые может принять каждая плата без возникновения ситуации переполнения;
- скорости передачи данных.
2.3. Глобальная сеть Internet
Наиболее распространенные сетевые протоколы
Определение. Протоколы являются набором правил и процедур, предназначенных для установления связей в сети.
Набор протоколов сети Internet, TCP/IP (Transmit Control Protocol / Internet Protocol) является промышленным стандартом протоколов, обеспечивающих связь компьютеров разных типов.
Основные протоколы передачи данных высокого уровня :
WWW (World Wide Web) – важнейший ресурс Internet, обеспечивающий гипертекстовое представление информации и гипертекстовые ссылки для единого представления и доступа во всемирной глобальной сети.
Gopher – усовершенствованная система передачи файлов. Позволяет, используя систему меню, просматривать списки ресурсов, пересылать нужный материал, просматривать данные. Компьютеры, использующие Gopher, можно представить соединенными в единую информационно-поисковую систему GopherSpace.
WAIS – индексная поисковая система глобального информационного сервера.
SNMP (Simple Network Management Protocol) – протокол сети Internet для мониторинга сети и сетевых компонентов.
FTP (File Transfer Protocol) – протокол сети Internet для передачи файлов. Поддерживает процесс передачи файлов между локальным и удаленным компьютером. Имеет ряд команд, которые реализуют двунаправленную передачу двоичных и ASCII-файлов между компьютерами.
Telnet – протокол сети Internet для регистрации на удаленных хостах и обработки данных на них.
SMTP (Simple Mail Transfer Protocol) – протокол сети Internet для обмена электронной почтой.
TCP (Transmission Control Protocol) – TCP/IP – протокол для гарантированной доставки данных, разбитых на последовательность фрагментов.
IP (Internet Protocol) – протокол сетевого уровня из набора протоколов Internet, обеспечивающий правильную передачу пакетов. IP является базовым элементом технологии Internet. Его центральная часть – таблица маршрутов. Этот протокол использует таблицу маршрутов при принятии всех решений о маршрутизации IP-пакетов.
OSPF (Open Shortest Path First) – алгоритм маршрутизации, использующий состояние каналов, в его основе лежит алгоритм Дейкстры. OSPF вычисляет маршруты, учитывая количество маршрутизаторов, через которые пакет пройдет на пути к получателю, пропускную способность линии, трафик и стоимость.
Набор протоколов IPX/SPX и NWlink (Internetwork Packet Exchange / Sequenced Packet Exchange) – стэк протоколов, используемых в сетях Novell. Это относительно небольшой и быстрый протокол, поддерживающий маршрутизацию. NWlink – реализация IPX/SPX фирмой Microsoft для использования в качестве транспортного маршрутизируемого протокола.
Концепция сокетов
Сетевой сокет (network socket) во многом напоминает электрическую розетку. В сети имеется множество сокетов, причем каждый из них выполняет стандартные функции. Все, что поддерживает стандартный протокол, можно «подключить» к сокету и использовать для коммуникаций. Для электрической розетки не имеет значения, что именно вы подключаете – лампу или тостер, поскольку оба прибора рассчитаны на напряжение 220 Вольт и частоту 50 Герц. Несмотря на то, что электричество свободно распространяется по сети, все розетки в доме имеют определенное место. Подобным образом работают и сетевые сокеты, за исключением того, что электроны и почтовые адреса заменены на пакеты TCP/IP и IP-адреса. Internet Protocol (IP) является низкоуровневым протоколом маршрутизации, который разбивает данные на небольшие пакеты и рассылает их по различным сетевым адресам, что не гарантирует доставку вышеупомянутого пакета адресату. Transmission Control Protocol (TCP) является протоколом более высокого уровня, собирающим пакеты в одну строку, сортирующим и перетранслирующим их по мере необходимости, поддерживая надежную рассылку данных. Третий протокол, UNIX Domain Protocol (UDP), используется вместе с TCP и может применяться для быстрой, но ненадежной передачи пакетов.
Клиент/сервер
Под термином сервер подразумевается любой объект с общедоступными ресурсами. Клиентом называется любой другой объект, желающий получить доступ к определенному серверу. Взаимодействие между клиентом и сервером во многом подобно взаимодействию лампы и розетки. Электрическая сеть является сервером, а лампа является клиентом напряжения. Сервер постоянно предлагает свои «услуги», в то время как клиент волен в любое время отключиться от обслуживания.
В сокетах Berkley понятие сокета позволяет одному компьютеру обслуживать несколько различных клиентов одновременно, а также одновременно обрабатывать информацию различных типов. Это стало возможным после введения понятия порта, который является нумерованным сокетом на определенном компьютере. Серверу разрешено обслуживать несколько клиентов, подсоединенных к одному порту, но не одновременно. Для управления соединением нескольких клиентов процесс сервера должен быть многопоточным или иметь другие средства мультиплексирования одновременных операций ввода-вывода.
Зарезервированные сокеты
После физического подключения выбирается протокол высокого уровня, который зависит от используемого порта. Согласно спецификации протокола TCP/IP, первые 1024 порта резервируются для определенных задач. Порт номер 21 предназначен для протокола FTP, 23 – для Telnet, 25 – для электронной почты, 79 – для протокола finger, 80 – для HTTP, и т.д. Каждый протокол определяет, каким образом клиент должен взаимодействовать с портом. Например, протокол HTTP используется Web-броузерами и серверами для передачи гипертекстовых страниц и изображений. Работает он следующим образом. Когда клиент запрашивает файл от сервера HTTP (это действие известно под названием попадание – hit), он просто записывает имя файла в специальном формате в определенный порт и получает обратно содержимое файла. Сервер также возвращает код состояния, сообщающий клиенту о возможности удовлетворения запроса, и причину отказа.. Вот пример запроса клиентом файла /index.html, в ответ на который сервер передает содержимое файла.
СЕРВЕР КЛИЕНТ
Опрашивает порт 80 Подключается к порту 80
Определяет подключение Записывает «GET /index.html к серверу HTTP/1.0\n\n»
Считывает до второго символа
новой строки (\n)
Определяет команду GET как
известную команду и протокол HTTP/1.0.
Считывает файл /index.html
Записывает «HTTP/1.0 200 OK\n\n» («200» означает «дальше идет содержимое файла»)
Копирует содержимое файла в сокет Считывает файл и выводит его
Отключается Отключается
