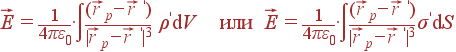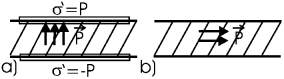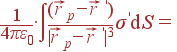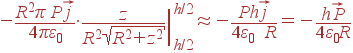Сегнетоэлектрики
М.И. Векслер, Г.Г. Зегря
Сегнетоэлектрики
представляют собой специфический класс сред, характеризующийся высоким
значением диэлектрической проницаемости (на основной кривой поляризации), нелинейностью
зависимости ![]() ,
гистерезисом зависимостей D(E) и P(E), а также сохранением поляризованности
,
гистерезисом зависимостей D(E) и P(E), а также сохранением поляризованности ![]() после
отключения внешнего поля. Именно последнее свойство наиболее важно, и во многих
случаях под словом "сегнетоэлектрик" подразумевается "область
спонтанной поляризованности
после
отключения внешнего поля. Именно последнее свойство наиболее важно, и во многих
случаях под словом "сегнетоэлектрик" подразумевается "область
спонтанной поляризованности ![]() ",
слабо чувствительная к дополнительному наложению электрического поля.
",
слабо чувствительная к дополнительному наложению электрического поля.
Расчет поля сегнетоэлектриков производится следующим образом. По формулам
|
|
(50) |
находится
связанный заряд, а затем находится создаваемое им поле ![]() с
помощью закона Кулона, как если бы этот заряд был свободным:
с
помощью закона Кулона, как если бы этот заряд был свободным:
|
|
(51) |
Если
есть выраженная симметрия, то возможно и применение теоремы Гаусса в виде ![]() .
Мотивацией такого метода является уравнение Максвелла
.
Мотивацией такого метода является уравнение Максвелла ![]() .
.
При наличии, помимо сегнетоэлектриков, еще и сторонних зарядов поле последних суммируется с полем сегнетоэлектриков.
Для
нахождения смещения ![]() привлекается
соотношение
привлекается
соотношение
|
|
(52) |
При этом никаких ε для сегнетоэлектрика вводиться не должно.
Задача.
Имеется бесконечная пластина из однородного сегнетоэлектрика с
поляризованностью ![]() .
Найти векторы
.
Найти векторы ![]() и
и
![]() внутри
и вне пластины, если вектор
внутри
и вне пластины, если вектор ![]() направлен
a) перпендикулярно, b) параллельно поверхности пластины.
направлен
a) перпендикулярно, b) параллельно поверхности пластины.
|
|
Решение
Разберемся прежде всего в том, какова будет ![]() в
обоих случаях, то есть какие связанные заряды присутствуют. Для этого надо
проверить, как изменяется
в
обоих случаях, то есть какие связанные заряды присутствуют. Для этого надо
проверить, как изменяется ![]() в
направлении самого себя. В случае б)
в
направлении самого себя. В случае б) ![]() ,
в том числе и на границах; на них
,
в том числе и на границах; на них ![]() ,
конечно, изменяется, но не в направлении
,
конечно, изменяется, но не в направлении ![]() .
А вот в случае а) имеет место скачок
.
А вот в случае а) имеет место скачок ![]() от
(до) нуля на границах как раз в направлении
от
(до) нуля на границах как раз в направлении ![]() .
Соответственно, поверхностная плотность заряда равна:
.
Соответственно, поверхностная плотность заряда равна:
|
σ'(a) = ± P |
причем
знак плюс берется для той поверхности, в сторону которой "смотрит"
вектор ![]() ,
по определению σ'. Как уже говорилось,
,
по определению σ'. Как уже говорилось,
|
σ'(b) = 0 |
Следовательно, в случае а) мы имеем ситуацию, аналогичную конденсатору и получаем
|
|
в то время как
|
|
Заметим,
что в случае а) ошибкой было бы записать D = σ'; теорема Гаусса
применяется к вектору ![]() .
.
Соответственно,
по формуле ![]() имеем:
имеем:
|
|
= |
|
|
|
|
= |
|
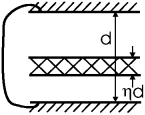
Задача. Пластина из сегнетоэлектрика с поляризованностью P, перпендикулярной поверхностям, помещена в конденсатор, обкладки которого замкнуты друг на друга. Пластина занимает η-ю часть зазора и параллельна обкладкам конденсатора. Найти E и D в пластине и в остающемся незаполненным зазоре.
|
|
Решение Если Eplate и Eair обозначают электрическое поле, соответственно, в пластине и в воздушном зазоре, то, ввиду замкнутости обкладок конденсатора друг на друга,
|
η Eplate +(1–η) Eair = 0 |
Величина D в зазоре и в пластине одна и та же, так как любой другой вариант противоречил бы условиям для нормальной компоненты D на границе пластина-воздух.
|
Dplate = ε0Eplate+P = Dair = ε0Eair |
Из последней цепочки равенств имеем
|
Eair = Eplate+ε0–1P |
Используя это, получаем
|
η Eplate +(1–η)(Eplate+ ε0–1P) = 0 |
откуда
|
Eplate = –(1–η)ε0–1P, Eair = ηε0–1P |
Смещение всюду одно и то же и равно Dplate = Dair = η P.
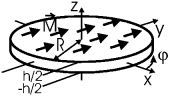
Задача.
Тонкий диск радиуса R из сегнетоэлектрического материала поляризован однородно
и так, что вектор ![]() лежит
в плоскости диска. Найти
лежит
в плоскости диска. Найти ![]() и
и
![]() в
центре диска, считая, что толщина диска h намного меньше, чем R.
в
центре диска, считая, что толщина диска h намного меньше, чем R.
|
|
Решение
Введем систему координат так, чтобы плоскость xy была плоскостью диска, а ![]() .
Найдем связанные заряды.
.
Найдем связанные заряды. ![]() всюду
равна нулю, за исключением обода диска (на круглых поверхностях диска тоже
всюду
равна нулю, за исключением обода диска (на круглых поверхностях диска тоже ![]() ,
так как там
,
так как там ![]() не
меняется в направлении
не
меняется в направлении ![]() ).
Поверхностный заряд составит
).
Поверхностный заряд составит
|
σ' = –Pr|R+0+Pr|R–0 = Psinφ |
где
φ угол в полярной системе координат, отсчитываемый от оси x, как обычно.
Зная σ', можно найти поле ![]() по
закону Кулона (
по
закону Кулона (![]() ):
):
|
|
= |
|
|
|
= |
|
||
|
= |
|
При
получении последнего равенства использовано условие R>> h. Обратим
внимание на то, что при R→∞ ![]() .
.
Смещение
![]() найдется
просто как
найдется
просто как
|
|
Список литературы
1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r
Дата добавления: 30.06.2011