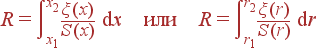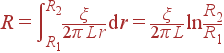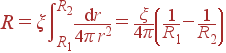Утечка заряда в конденсаторах
М.И. Векслер, Г.Г. Зегря
Диэлектрик в конденсаторе обладает конечным удельным (Ом·см) сопротивлением ξ, которое может зависеть от координат. Ток через конденсатор при U0 = const составляет
|
|
(46) |
где в случае ξ = ξ(x) или ξ = ξ(r)
|
|
(47) |
S(x) (или S(r)) обозначает площадь эквипотенциальной поверхности. Если батарею отключить, то напряжение на конденсаторе будет спадать по закону
|
|
(48) |
где C - емкость. Отсюда получаем
|
|
(49) |
Задача. Найти сопротивление R цилиндрического конденсатора (R1, R2, L, ξ = сonst).
Решение: Эквипотенциальные поверхности - это боковые цилиндрические поверхности, площадь каждой из которых
|
S = 2π L r |
Поскольку ξ = const, по формуле для сопротивления получаем:
|
|
Задача: Напряжение на сферическом конденсаторе емкости C (R1, R2) после отсоединения его от батареи спало в η раз за время Δ t. Найти удельное сопротивление диэлектрика (диэлектрик считать однородным).
Решение: Омическое сопротивление описанного конденсатора равно
|
|
где ξ - искомое удельное сопротивление.
Если t = 0 соответствует моменту отсоединения батареи, то, как следует из условия, напряжение на конденсаторе в момент t = Δ t составляет U0/η (U0 - начальное напряжение):
|
|
откуда получается
|
|
Приравнивая это R и выражение для того же R через ξ, имеем
|
|
Задача: Напряжение на цилиндрическом конденсаторе с радиусами обкладок R1, R2 и длиной L спало в η раз за время Δ t после отсоединения конденсатора от батареи. Найти удельное сопротивление диэлектрика (диэлектрик однороден и имеет проницаемость ε).
Ответ:
![]() (нет зависимости от R1, R2, L).
(нет зависимости от R1, R2, L).
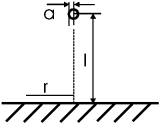
Задача. В диэлектрике проницаемости ε на расстоянии l от бесконечной проводящей плоскости расположен небольшой металлический шарик радиуса a<< l. Найти ток, если между шариком и плоскостью поддерживается разность потенциалов U, а удельное сопротивление среды ξ.
|
|
Решение Ток может быть найден в любом эквипотенциальном сечении. Например, можно вычислить ток непосредственно на плоскости, с использованием составляющей электрического поля, перпендикулярной к плоскости и легко вычисляемой методом изображений:
|
|
Мы здесь считаем заряд точечным, так как поле ищется далеко от него.
|
|
Чтобы связать q с приложенным напряжением, нужно знать емкость C, которая уже найдена в разделе "Вычисление емкости": C = 4πε0ε a. Получается, что
|
|
Эта задача могла быть решена и проще: сопротивление R между шариком и плоскостью сосредоточено, в основном, вблизи шарика. Тогда при его вычислении можно грубо считать поле вокруг шарика сферически-симметричным, что дает
|
|
после чего ток найдется как I = U/R. Однако, применение такого метода предварительного нахождения R, например, в похожей задаче, в которой вместо заряда задан провод, уже невозможно, в то время как способ интегрирования тока вблизи плоскости остается вполне состоятельным.
Список литературы
1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r
Дата добавления: 30.06.2011