Расслоенные пространства внутренних степеней свободы
[ 1 ] с
координатами 
( 
= 1,2): 
1 -
внутренняя энергия 
, 
- тепло 
. Введем слоевые координаты 
и 
, где t - абсолютная температура
T, 
- молярная теплоемкость при постоянном объеме
и 
- молярная теплоемкость при постоянном давлении 
. Итак, слоевое пространство 
имеет N = 2 измерений. Пусть 
, тогда имеем дело с векторным полем.
Введем метрическую функцию 
в каждой точке 
, которая является однородной функцией степени один в слоевых координатах и однородной
функцией степени нуль в базовых координатах. Чтобы такого добиться, следует еще ввести постоянную составляющую вектора 
. Исходя из физических соображений, такой составляющей вектора может служить величина 
, являющаяся универсальной газовой постоянной R. Таким образом, мы переходим к слоевому
пространству c N + 1 измерений. Подобное наблюдается в СТО, где вводится скорость света с и переходят четырехмерному пространству. Функция 
определяет длину вектора 
. Удобно перейти к функции
= 
, которая является однородной функцией степени два в слоевых
координатах. Составляющие метрического тензора в общем случае определяются по формуле [ 2]
, где 
=
.
Это есть однородные функции степени нуль в слоевых координатах.
Тогда
и 
.
В точке 
имеется и пространство 
с координатами 
, которые определяются следующим образом
Имеем
, 
Параллельный перенос будет, если 
= 0 и 
= 0.
В качестве модельного дифференциального уравнения привлекаем уравнение типа модифицированного нелинейного дифференциального уравнения Кортевега - де Вриза, которое хорошо изучено. Этим уравнением мы описываем термоэлектрическое состояние:
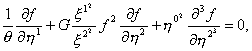
где 
- безразмерная постоянная, 
– диэлектрическая проницаемость. Она является безразмерной величиной. Если же среда анизотропная,
то диэлектрическую проницаемость могли составлять величины 
. Ограничимся классом решений 
, где 
, то
есть 
. Тогда одним из решений данного уравнения будет являться
функция 
Построим функцию 
следующим образом:
, где 
.
Тогда нелинейные дифференциальные уравнение для L и F2 представляется в форме:
Каждое дифференциальное уравнение индуцирует соответствующей структуры пространство [ 3 ]. В данном случае решение дифференциального уравнения сводится к поиску геометрических структур данного пространства.
Введем обозначение
В выделенном классе решений получаем следующие дифференциальные уравнения слоевых координат пространства 
:
Имеем и следующие значения слоевых координат (составляющие ковариантного
вектора 
):
, 
где 
.
Проверим правильность нахождения векторов 
. Должно иметь силу
соотношение 
. Имеем
Составляющие 
определены
правильно.
В рассматриваемом классе решений получаем следующие нелинейные дифференциальные уравнения для составляющих метрического
тензора 
:
.
Тогда составляющие коэффициентов связностей 
находится по
формулам:
В итоге получаем составляющие метрического тензора
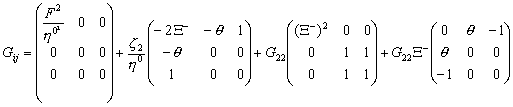
И составляющие коэффициентов связностей:
, 
,
.
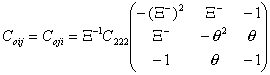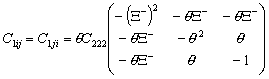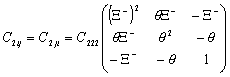Проверка правильности найденных составляющих метрического тензора производится традиционным способом, а именно,
в выражение 
следует подставить
конкретные значения для составляющих метрического тензора и получить квадрат метрической функции. Подстановка в данное выражение найденных здесь составляющих
метрического тензора приводит к квадрату метрической функции.
Проверка правильности найденных здесь составляющих связностей производится посредством достижения выполнения
условия Эйлера 
.
Найденные здесь значения метрического тензора приводят к выполнению данного условия .
Определим коэффициенты
.
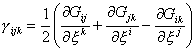Поставим конкретные значения для составляющих метрического тензора. Получаем
| |
,
, 
.
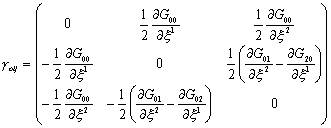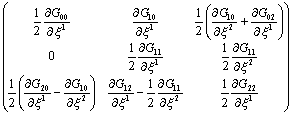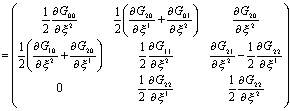Составляющие этих матрицы сводятся к 
, 
и 
.
Используя производные от этих величин, получаем конкретные значения 
:
, 
.
Определим величины 
, входящие в уравнение геодезических, по формуле [ 2 ]:
Имеем
Используя формулы:
Получаем для 
и 
:
Правильность введенных здесь значений для 
и 
можно проверить, если выполняется условие
Такое тождество выполняется при подстановке конкретных значений.
Определим коэффициенты 
и 
[ 2 ].
Существует связь [ 2 ]
Если 
, тогда
.
Речь идет о параллельном переносе составляющих вектора 
. Имеем
=
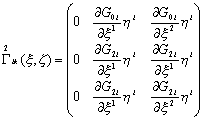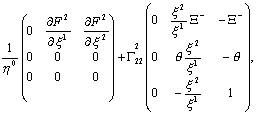
где 
В введенном пространстве могут быть определены переносы тензоров более высокого ранга по формулам, которые приведены в работах [ 1, 2 ].
Заключение. Построенные здесь геометрические структуры расслоенного пространства внутренних степеней свободы, ассоциируемого с термоэлектрическим состоянием. Возможно многообразие других термоэлектрических состояний. Речь идет о методе построения геометрических структур, об “офизичивании” геометрии расслоенных пространств. Привлечение в физику расслоенных пространств позволяет построить весьма корректно теории сложных физических систем с большой неоднородностью и анизотропией, с большой нелинейностью и находящихся в сильных физических полях.
1.Лаптев Б.Л. Ковариантный дифференциал и теория дифференциальных инвариантов в пространстве тензорных опорных элементов/Ученые записки. Том 118, кн.4, 1958, с. 75-147.
2.Рунд Х. Дифференциальная геометрия финслеровых пространств. Перевод с англ. под ред. Э.Г. Позняка.М.: 1981, 501 с.
3.Виноградов А.М., Красильщик И.С., Лычагин В.В. Введение в геометрию нелинейных дифференциальных уравнений. М.: Наука, 1986, 335 с.
