Задачи по моделированию с решениями
Задачи по моделированию с решениями
Задача №1.
Необходимо построить рекуррентный алгоритм моделирования, нормального случайного процесса, с заданной корреляционной функцией.
Метод решения, на основе факторизации.
Дано.
R(t) =![]() ;
;
![]()
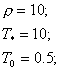 при
при ![]() ;
;
Корреляционная функция стационарного, случайного процесса с рациональным спектром, имеет вид:
R(![]() )=
)=![]() ;
;
![]()
![]() следовательно
система.
следовательно
система.
![]()
![]()
![]()
Корреляционная функция соответствующего дискретного процесса равна:
R[n]=![]()
где ![]()
![]()
![]() ;
; ![]() ;
;
где ![]() ; fb=
; fb=![]() fb=20;
fb=20;
![]()
Отсюда найдем:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
Не нарушая общности рассуждений,
положим ![]() , тогда R[0]=1. Запишем
функцию R[n] для n
, тогда R[0]=1. Запишем
функцию R[n] для n![]() 0 в комплексной форме:
0 в комплексной форме:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
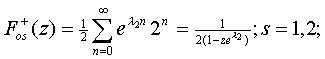
Отсюда
![]() ;
;
Следовательно, спектральная функция F(z) в соответствии имеет вид.
![]() ;
;
После приведения к общему знаменателю и приведения подобных членов получим.
![]() ;
;
где
![]()
![]()
![]() ,
, ![]() ;
;
Знаменатель F(z) представляет собой произведение двух сомножителей требуемой формы, т.е. в факторизации знаменателя нет надобности. Это всегда будет иметь место при использовании такой последовательности подготовительной работы.
Для факторизации числителя найдем его корни:
![]() ;
;
![]() ;
;
В данном случае ввиду симметрии уравнения
![]() ;
;
анализ корней для уяснения
величины их модуля не потребуется, и в качестве корня ![]() окончательного
выражения вида брать любой из корней
окончательного
выражения вида брать любой из корней ![]() . В этом можно убедится, подставив в уравнение
. В этом можно убедится, подставив в уравнение ![]() вместо
вместо ![]() значения корней.
Действительно, уравнение обращается в тождество при
значения корней.
Действительно, уравнение обращается в тождество при ![]() .
.
Таким образом, дискретная
передаточная функция формирующего фильтра и рекуррентный алгоритм для
моделирования случайного процесса с корреляционной функцией ![]() имеют соответствующий
вид
имеют соответствующий
вид
![]() ;
;
![]() ; где
; где
![]() ,
, ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
;
![]()
![]() .
.
Задача №2.
 |
Дана структура нелинейного фильтра, схема которого представлена выше.
 |
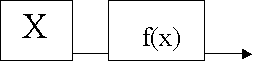 |
|||
|
|
|||
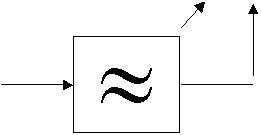
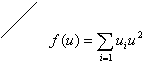 |
Схема измерительной структуры представлена выше.
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.cooldoclad.narod.ru/
Дата добавления: 13.08.2003


