Анализ и выбор решений на основе нечеткой монотонной экспертной информации
Анализ и выбор решений на основе нечеткой монотонной экспертной информации
Л.С. Берштейн, А.В. Боженюк
Перед разработчиками экспертных систем (ЭС) в области искусственного интеллекта стоят, как правило, следующие три задачи: выбор представления экспертной информации о предметной области в системе; выбор и (или) обоснование подхода к принятию решения (ПР) на основе этой информации; разработка алгоритмов, реализующих выбранный подход к ПР.
В случае, когда при решении первой задачи используется нечеткое представление информации (в терминах нечетких и лингвистических переменных), возникают задачи оценки этой информации на предмет ее непротиворечивости (или оценки степени ее непротиворечивости), а также задачи соотношения этой информации и желаемой точности получения результата. Это указывает на необходимость предварительного анализа нечеткой экспертной информации. Данный анализ позволил бы:.
1.Оценить соответствие имеющейся нечеткой информации требованиям, которым по мнению пользователя ЭС, должны удовлетворять получаемые решения;
2. Найти "узкие места" такой информации с целью ее корректировки (например, путем задания дополнительных вопросов эксперту о выборе решения в таких "местах").
Для проведения такого анализа введем понятия отношение упорядочения на значениях лингвистической переменной и монотонности нечеткой экспертной информации.
Определение 1. Пусть ![]() - лингвистическая переменная [1], определенная на множестве Х
и имеющая базовые значения
- лингвистическая переменная [1], определенная на множестве Х
и имеющая базовые значения ![]() ,
, ![]() . Здесь
. Здесь ![]() - нечеткие переменные с унимодальными функциями
принадлежности
- нечеткие переменные с унимодальными функциями
принадлежности ![]() ,
, ![]() . Введем на множестве
базовых значений Т отношение упорядочения
. Введем на множестве
базовых значений Т отношение упорядочения ![]() следующим образом:
следующим образом:
![]() .
.
Иными словами ![]() , если значение
, если значение ![]() , для которого функция принадлежности принимает свое
наибольшее значение 1, не больше значения , на котором функция
, для которого функция принадлежности принимает свое
наибольшее значение 1, не больше значения , на котором функция ![]() также принимает
значение 1.
также принимает
значение 1.
Определение 2. Обозначим
через ![]() - обобщенную лингвистическую
переменную, принимающую значения
- обобщенную лингвистическую
переменную, принимающую значения ![]()
![]() . Пусть
. Пусть ![]() , а
, а ![]() .
.
Будем считать, что:
![]() .
.
Пусть процесс ПР
характеризуется выбором некоторого значения
параметра V, на которое влияют
значения параметров X, Y,...,Z. Введя лингвистические переменные ![]() ,
, ![]() ,
, ![]() ,...,
,..., ![]() с множеством базовых значений соответственно
с множеством базовых значений соответственно ![]() ,
, ![]() ,
, ![]() ,..., и
,..., и ![]() экспертную информацию
о выборе решения представим в виде системы нечетких высказываний
экспертную информацию
о выборе решения представим в виде системы нечетких высказываний ![]() :
:
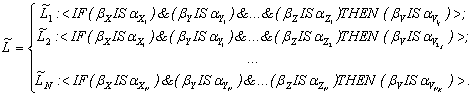
Здесь ![]() ,
, ![]() ,...,
,..., ![]() и
и ![]() .
.
Фактически нечеткая
система высказываний ![]() представляет собой некоторую функцию
представляет собой некоторую функцию ![]() , определенную на множестве базовых значений обобщенной
лингвистической переменной.
, определенную на множестве базовых значений обобщенной
лингвистической переменной.
Зафиксируем произвольные
значения ![]() ,
, ![]() ,...,
,..., ![]() .
.
Определение 3. Систему нечетких высказываний ![]() назовем монотонной по параметру X, если справедливо
выражение:
назовем монотонной по параметру X, если справедливо
выражение:
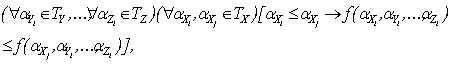 или
или
![]()
Определение 4. Систему
нечетких высказываний ![]() монотонную по всем параметрам X, Y,...,Z, назовем просто монотонной нечеткой
системой.
монотонную по всем параметрам X, Y,...,Z, назовем просто монотонной нечеткой
системой.
Свойство 1. Для того,
чтобы система нечетких высказываний ![]() была монотонной, необходимо и достаточно, чтобы выполнялось условие:
была монотонной, необходимо и достаточно, чтобы выполнялось условие:
![]()
или
![]()
В работе [2] была
предложена общая схема выбора значений параметров при нечеткой экспертной
информации. Согласно ей, при заданных входных параметрах X, Y,...,Z, выбирается
такое подмножество ![]() значений выходного
параметра V, для элементов которого степень истинности правила modus ponens
для нечеткой схемы вывода
значений выходного
параметра V, для элементов которого степень истинности правила modus ponens
для нечеткой схемы вывода
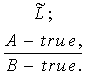 (1)
(1)
принимает свое
наибольшее значение. Здесь ![]() - система нечетких экспертных высказываний.
- система нечетких экспертных высказываний. ![]() - высказывание типа
- высказывание типа ![]() . Величины x,y,...,z - конкретные значения входных параметров
X, Y,...,Z.
. Величины x,y,...,z - конкретные значения входных параметров
X, Y,...,Z. ![]() - высказывание типа
- высказывание типа ![]() , величина v - значение из подмножества
, величина v - значение из подмножества ![]() .
.
Степень истинности правила modus ponens для схемы вывода (1) определится выражением:
![]() . (2)
. (2)
где n - число
высказываний в системе ![]() .
.
Свойство 2. Для заданных значений x, y,...,z входных параметров функция ![]() является непрерывной
на множестве значений параметра V.
является непрерывной
на множестве значений параметра V.
Свойство 3. Если система ![]() обладает свойством
монотонности, то функция унимодальна, или достигает своего максимума на
некотором интервале множества значений параметра V.
обладает свойством
монотонности, то функция унимодальна, или достигает своего максимума на
некотором интервале множества значений параметра V.
Обозначим через ![]() . Тогда выражение (2) можно переписать в виде:
. Тогда выражение (2) можно переписать в виде:
![]() ,
,
где m - множество
базовых значений лингвистической переменной
![]() .
.
Свойство 4. Если система
![]() обладает свойством
монотонности, то справедливы неравенства
обладает свойством
монотонности, то справедливы неравенства
![]() , при
, при ![]() ,
,
![]() , при
, при ![]() .
.
Данное свойство
позволяет предложить следующие алгоритмы нахождения значений параметра V, для
которых величина степени истинности ![]() достигает своего
наибольшего значения.
достигает своего
наибольшего значения.
Отсортируем вначале
значения ![]() в порядке их
увеличения. Будем считать, что
в порядке их
увеличения. Будем считать, что ![]() , где
, где ![]() соответствует некоторому
соответствует некоторому ![]() .
.
Рассмотрим вначале
алгоритм для более простого случая. Пусть ![]() - носители нечетких множеств, соответствующие нечетким
перемен-ным
- носители нечетких множеств, соответствующие нечетким
перемен-ным ![]() . Пусть выполняется условие:
. Пусть выполняется условие:
![]() . (3)
. (3)
Иными словами, для любого значения параметра V число функций принад-лежности, одновременно не равных 0, не превышает двух. Пример такого случая показан на рис.1.
При выполнении условия
(3), алгоритм определения множества значений ![]() параметра V, будет
иметь вид:
параметра V, будет
иметь вид:
![]() . Определяем подмножество
. Определяем подмножество ![]() , для элементов которого справедливо выражение:
, для элементов которого справедливо выражение: ![]() .
.
Если подмножество, то ![]() и
и ![]() . Переход на.
. Переход на. ![]()
![]() . Если
. Если ![]() , то определяем
единственное значение
, то определяем
единственное значение ![]() , при котором выполняется условие:
, при котором выполняется условие: ![]() . В этом случае
. В этом случае ![]() .
.
![]() . Конец.
. Конец.
Заметим, что п. ![]() всегда выполним, так
как согласно свойству 4, функции принадлежности
всегда выполним, так
как согласно свойству 4, функции принадлежности ![]() и
и ![]() соответствуют
"соседним" нечетким переменным
соответствуют
"соседним" нечетким переменным ![]() и
и ![]() у которых
у которых ![]() .
.
Рассмотрим теперь
алгоритм для более сложного случая, когда условие (3) может не выполняться. В
этом случае, алгоритм определения множества значений ![]() параметра V, примет
вид:
параметра V, примет
вид:
![]() . Определяем подмножество
. Определяем подмножество ![]() , для элементов
которого справедливо
, для элементов
которого справедливо ![]() .
.
Если подмножество ![]() , то
, то ![]() и
и ![]() . Переход на
. Переход на ![]() .
.
![]() . Определяем подмножество
. Определяем подмножество ![]() , для элементов
которого справедливо
, для элементов
которого справедливо ![]() .
.
Если подмножество ![]() , то
, то ![]() и
и ![]() . Переход на
. Переход на ![]() .
.
![]() . Если
. Если ![]() , то определяем единственное значение
, то определяем единственное значение ![]() , при котором
выполняется условие:
, при котором
выполняется условие: ![]() . В этом случае
. В этом случае ![]() .
.
![]() . Конец.
. Конец.
Рассмотренные алгоритмы
значительно проще алгоритма, предложенного в [1] для произвольных (не
монотонных) систем высказываний ![]() .
.
Список литературы
Модели принятия решений на основе лингвистической переменной / А.Н.Борисов, А.В.Алексеев, О.А.Крумберг и др. Рига: Зинатне,1982.-256с.
Нечеткие модели для экспертных систем в САПР / Н.Г.Малышев, Л.С.Берштейн, А.В.Боженюк. - М.:Энергоатомиздат,1991.-136с.
Дата добавления: 14.04.2005


