Подстановки
Представлены понятия подстановки, умножения подстановок, единичной подстановки, четной и нечетной подстановок, транспозиции, лемма о нечетности транспозиции, знак подстановки, теорема о знаке произведения, свойства знаков подстановок
п.1. Симметрическая группа степени n.
Обозначим ![]() , где
, где ![]() .
.
Определение. Симметрическая группа, определённая на
множестве ![]() , называется
симметрической группой степени
, называется
симметрической группой степени ![]() . Элементами
этой группы являются биекции, которые множество
. Элементами
этой группы являются биекции, которые множество ![]() , которые
называются подстановками степени
, которые
называются подстановками степени ![]() .
.
По традиции подстановки принято обозначать маленькими
греческими буквами. Пусть ![]() - множество
всех подстановок степени
- множество
всех подстановок степени ![]() .
. ![]() ,
, ![]() - биекция.
Подстановки принято записывать в виде таблицы из двух строк в следующем виде:
- биекция.
Подстановки принято записывать в виде таблицы из двух строк в следующем виде: ![]()
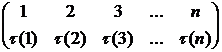 . Каждая
подстановка
. Каждая
подстановка ![]() степени
степени ![]() кодируется кортежем
кодируется кортежем ![]() , который
является перестановкой
, который
является перестановкой ![]() -ого множества
-ого множества
![]() , поэтому число
всех подстановок степени
, поэтому число
всех подстановок степени ![]() равно
равно ![]() , то есть
, то есть ![]()
Определение. Умножением подстановок называется их композиция.
Определение. Единичной (тождественной) подстановкой
называется подстановка 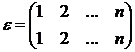 . Единичная
подстановка все элементы оставляет на месте. Для каждой подстановки
. Единичная
подстановка все элементы оставляет на месте. Для каждой подстановки ![]() определена обратная подстановка
определена обратная подстановка ![]()
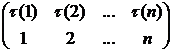
Теорема 1. Алгебра, определенная на множестве ![]() есть группа, которая называется группой
подстановок степени
есть группа, которая называется группой
подстановок степени ![]() , порядок
группы равен
, порядок
группы равен ![]() .
.
п.2. Чётные и нечётные подстановки.
Пусть ![]() ,
, ![]()
![]()
![]()
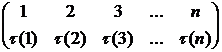
Определение. Пусть ![]() -
упорядоченная пара такая, что
-
упорядоченная пара такая, что ![]() . Пара
. Пара ![]() называется инверсией подстановки
называется инверсией подстановки ![]() , если
, если ![]()
Определение. Подстановка ![]() называется чётной, если она содержит чётное
число инверсий
называется чётной, если она содержит чётное
число инверсий ![]() .
.
![]() - чётные
подстановки.
- чётные
подстановки.
Подстановка ![]() называется нечётной, если она содержит нечётное
число инверсий
называется нечётной, если она содержит нечётное
число инверсий
![]() - не чётные
подстановки.
- не чётные
подстановки.
Определение. Транспозицией называются те подстановки,
которые переставляют только два элемента множества ![]() . Другими
словами, транспозициями называют подстановки
. Другими
словами, транспозициями называют подстановки ![]() вида
вида ![]()
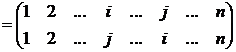 , где
, где ![]() ,
, ![]() ,
, ![]() и все элементы, неравные
и все элементы, неравные ![]() ,
, ![]() остаются на месте под действием подстановки
остаются на месте под действием подстановки ![]() .
.
Пример.
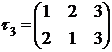 является транспозицией.
является транспозицией.
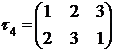 не является транспозицией.
не является транспозицией.
Лемма 1. Любая транспозиция есть нечётная подстановка.
Доказательство. Рассмотрим транспозицию ![]() , имеющую вид
, имеющую вид 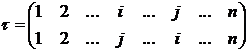
![]()
![]()
![]()
![]() .
.
Рассмотрим пару ![]() , где
, где ![]() .
.
Если ![]() , то
, то ![]()
![]()
![]() - не инверсия,
- не инверсия,
значит инверсией могут быть только те пары ![]() , где
, где ![]() или
или ![]() совпадают с одним из чисел
совпадают с одним из чисел ![]() или
или ![]() .
.
Пусть ![]() ,
, ![]() (так как
(так как ![]() -
транспозиция). Тогда для пары
-
транспозиция). Тогда для пары
![]() имеем
имеем ![]()
![]()
![]()
![]() пары
пары ![]() не образуют инверсию.
не образуют инверсию.
Пусть ![]() ,
, ![]() . Для пары
. Для пары ![]() , где
, где ![]() возможны случаи:
возможны случаи:
а) пусть ![]() ,
, 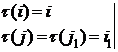
![]()
![]()
![]() пары
пары ![]() , где
, где ![]() инверсии не образуют.
инверсии не образуют.
б) ![]() ,
, ![]() имеем, если
имеем, если ![]() , то пара
, то пара ![]() - инверсия.
- инверсия.
Если ![]() , то
, то ![]()
![]()
![]() , значит все
пары
, значит все
пары ![]() такие, что
такие, что ![]() будут инверсиями. Число таких пар равно числу
целых чисел на полуоткрытом интервале
будут инверсиями. Число таких пар равно числу
целых чисел на полуоткрытом интервале ![]() , потому что
число инверсий указанного вида будет
, потому что
число инверсий указанного вида будет ![]() .
.
Мы подсчитали число инверсий ![]() таких, что
таких, что ![]() или
или ![]() .
.
Подсчитаем теперь число инверсий ![]() таких, что
таких, что ![]() и
и ![]() , возможны
случаи:
, возможны
случаи:
IV. ![]() ,
, ![]() имеем
имеем 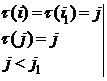
![]()
![]() . Все такие
пары образуют инверсию, число таких инверсий равно числу целых чисел в
интервале
. Все такие
пары образуют инверсию, число таких инверсий равно числу целых чисел в
интервале ![]() , поэтому
число таких инверсий равно
, поэтому
число таких инверсий равно ![]()
V. ![]() ,
, ![]() ,
, 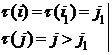
![]()
![]() , значит такие
пары не образуют инверсии.
, значит такие
пары не образуют инверсии.
VI. ![]() имеем
имеем 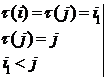
![]()
![]() , значит такие
пары не образуют инверсии.
, значит такие
пары не образуют инверсии.
Следовательно, общее число инверсий в транспозиции ![]() - это число
нечётное, значит транспозиция
- это число
нечётное, значит транспозиция ![]() нечётная подстановка. Лемма доказана.
нечётная подстановка. Лемма доказана.
Пусть ![]() ,
, ![]() - множество
всех подстановок степени
- множество
всех подстановок степени ![]() .
.
Определение. Функция ![]() и
и 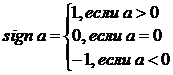 называется знаком числа
называется знаком числа ![]() .
.
Теорема 1. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Знак
произведения равен произведению знаков.
. Знак
произведения равен произведению знаков.
Доказательство.
если ![]() или
или ![]() , то
, то ![]() и знак числа равен 0
и знак числа равен 0
пусть ![]() и
и ![]() . Возможны
случаи:
. Возможны
случаи:
а) ![]()
![]()
![]()
б) ![]()
![]()
![]()
![]()
в)![]()
![]()
![]()
![]()
г) ![]()
![]()
![]()
![]()
Определение. Функцией знак подстановки называется
функция ![]()
![]() .
.
Пусть ![]()
1) 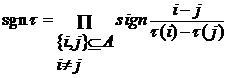 . Знак
подстановки
. Знак
подстановки ![]() равен произведению знаков чисел
равен произведению знаков чисел ![]()
Доказательство. Рассмотрим пару ![]() , где
, где ![]() . Пусть пара
. Пусть пара ![]() - инверсия,
тогда числитель и знаменатель дроби
- инверсия,
тогда числитель и знаменатель дроби ![]() имеют разные знаки, тогда
имеют разные знаки, тогда ![]() . Если пара
. Если пара ![]() не является инверсией в подстановке
не является инверсией в подстановке ![]() , то
, то ![]() , тогда
, тогда ![]() , поэтому
, поэтому 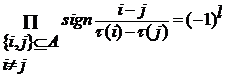 , где
, где ![]() - число инверсий, поэтому
- число инверсий, поэтому 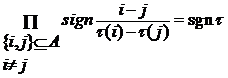 .
.
2) знак произведения двух подстановок равен
произведению знаков этих подстановок, то есть ![]()
![]() .
.
Доказательство. Запишем 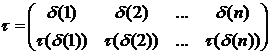 , тогда
, тогда 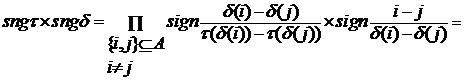
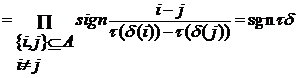
Теорема 2. Функция знак подстановки обладает свойствами:
1) ![]()
![]()
2) если ![]() -
транспозиция, то
-
транспозиция, то ![]()
3) ![]()
![]()
4) ![]() если
если ![]() -
транспозиция, то знак подстановки
-
транспозиция, то знак подстановки ![]()
Доказательство.
Пусть ![]() ,
, ![]() - единичная
подстановка,
- единичная
подстановка, ![]() . Справедливо
равенство:
. Справедливо
равенство: ![]() (
(![]() - должны быть
одного знака)
- должны быть
одного знака) ![]()
![]() .
.
![]()
Следствие 1. Произведение подстановок одинаковой чётности – чётная подстановка.
Следствие 2. Произведение подстановок разной чётности – не чётная подстановка.
Следствие 3. Множество чётных подстановок относительно
операций ![]() - единичные
подстановки образуют группу – группу чётных подстановок.
- единичные
подстановки образуют группу – группу чётных подстановок.
п.4. Разложение подстановок. Произведение циклов.
Определение. Подстановка ![]() называется циклом, если существует
называется циклом, если существует ![]() :
: ![]() ,
, ![]() ,
, ![]() а остальные элементы
а остальные элементы ![]() остаются на месте. Цикл записывается в виде
остаются на месте. Цикл записывается в виде ![]() ,
, ![]() - длина цикла.
Каждая транспозиция является циклом длины 2.
- длина цикла.
Каждая транспозиция является циклом длины 2.
Определение. Два цикла называются независимыми, если
они не имеют общих действительно перемещаемых символов. 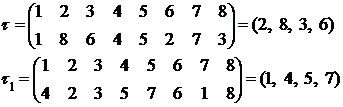
![]() ,
, ![]() - независимые
циклы.
- независимые
циклы.
каждая подстановка единственным образом с точностью до
порядка сомножителей раскладывается произведением независимых циклов 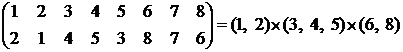
независимые циклы попарно коммутируют, то есть если ![]() и
и ![]() - независимые
циклы, то
- независимые
циклы, то ![]()
каждая подстановка есть произведение транспозиции: ![]() или
или ![]()
![]()
Каждая перестановка множества ![]() может быть получена из перестановки
может быть получена из перестановки ![]() последовательной перестановкой двух элементов.
последовательной перестановкой двух элементов.
Доказательство.
Докажем равенство ![]()
![]() .
Транспозиция- это цикл длины 2. Равенство
.
Транспозиция- это цикл длины 2. Равенство ![]()
![]() - это
равенство функций.
- это
равенство функций.
Область определения функций в левой и правой частях
равенства равны. Проверим, что эти функции принимают одинаковые значения на
одинаковых элементах. Значение левой подстановки от ![]() равно
равно ![]() по определению цикла. В правой части –
композиция. Сначала на
по определению цикла. В правой части –
композиция. Сначала на ![]() действует внутренняя подстановка – она
переводит
действует внутренняя подстановка – она
переводит ![]() в
в ![]() , в следующих
подстановках нет
, в следующих
подстановках нет ![]() , поэтому они
оставляют
, поэтому они
оставляют ![]() на месте, значит подстановка в правой части
на месте, значит подстановка в правой части ![]() перевела в
перевела в ![]() . Рассмотрим
как действует подстановка на элемент
. Рассмотрим
как действует подстановка на элемент ![]() . Левая
подстановка
. Левая
подстановка ![]() переводит в
переводит в ![]() по определению цикла. В правой подстановке
последняя внутренняя подстановка
по определению цикла. В правой подстановке
последняя внутренняя подстановка ![]() переводит в
переводит в ![]() , так как
подстановка
, так как
подстановка ![]() - биекция.
Предпоследняя внутренняя
- биекция.
Предпоследняя внутренняя ![]() переводит в
переводит в ![]() . Следующие
подстановки (транспозиции)
. Следующие
подстановки (транспозиции) ![]() оставляют на месте, так как в них нет
оставляют на месте, так как в них нет ![]() , значит
правая подстановка
, значит
правая подстановка ![]() переводит в
переводит в ![]() . Таким
образом, значения левой и правой подстановок в равенстве равны. Рассмотрим как
действуют подстановки на элемент
. Таким
образом, значения левой и правой подстановок в равенстве равны. Рассмотрим как
действуют подстановки на элемент ![]() . Левая
подстановка
. Левая
подстановка ![]() переводит в
переводит в ![]() (по определению цикла). Последняя внутренняя
(по определению цикла). Последняя внутренняя ![]() оставляет на месте, вторая внутренняя
оставляет на месте, вторая внутренняя ![]() переводит в
переводит в ![]() , третья
внутренняя
, третья
внутренняя ![]() переводит в
переводит в ![]() . Значит
правая внутренняя подстановка
. Значит
правая внутренняя подстановка ![]() переводит в
переводит в ![]() . Таким
образом, значения левой и правой подстановок равенства на элементе
. Таким
образом, значения левой и правой подстановок равенства на элементе ![]() равны.
равны.
Рассмотрим, как действуют подстановки на элемент ![]() . Левая
подстановка
. Левая
подстановка ![]() переводит в
переводит в ![]() (по определению цикла), правая подстановка
(по определению цикла), правая подстановка ![]() переводит в
переводит в ![]() . Получили,
что числа
. Получили,
что числа ![]() правая и левая подстановки в равенстве
правая и левая подстановки в равенстве ![]() переводят одинаково, остальные числа они
оставляют на месте. То есть все одинаковые элементы подстановки в равенстве
переводят одинаково, остальные числа они
оставляют на месте. То есть все одинаковые элементы подстановки в равенстве ![]()
![]() переводят одинаково.
переводят одинаково.
Вывод: функции в равенстве ![]()
![]() равны.
равны.
знак цикла ![]()
Доказательство. В формуле ![]()
![]() все транспозиции в правой части – нечётные
подстановки. Их
все транспозиции в правой части – нечётные
подстановки. Их ![]() , тогда знак
, тогда знак ![]() .
.
Пример.
получить из перестановки ![]() другую перестановку
другую перестановку ![]() последовательно переставляя по два элемента.
последовательно переставляя по два элемента.
Решение.
Составим подстановку: первую перестановку- в первую строку, вторую перестановку- во вторую строку. Разложим эту подстановку произведением циклов
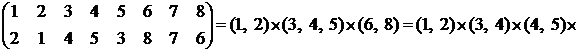
![]() .
.
В перестановке ![]() поменяем местами символы 6 и 8. Получим
поменяем местами символы 6 и 8. Получим ![]() ; меняем 4 и
5, получаем перестановку
; меняем 4 и
5, получаем перестановку ![]() ; меняем 3 и
4, получим
; меняем 3 и
4, получим ![]() ; меняем 1 и
2, получим
; меняем 1 и
2, получим ![]() .
.
Получить из перестановки ![]() другую перестановку
другую перестановку ![]() ,
последовательно переставляя по два элемента
,
последовательно переставляя по два элемента 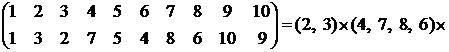
![]()
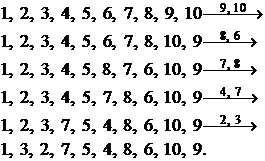
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Дата добавления: 05.10.2011


