Современные качественные исследования устойчивости

И.А. Колесникова

Российский университет дружбы народов

О вариационности некоторых ДУЧП  с отклоняющимися аргументами

Исследована задача существования вариационных принципов для дифференциальных уравнений с отклоняющимися аргументами вида  

1. Постановка задачи. Пусть N – оператор, заданный в области D(N) линейного нормированного пространства U над полем действительных чисел R, а область значений R(N)  принадлежит линейному нормированному пространству V над полем R, т.е.

В дальнейшем всюду предполагается, что в каждой точке

 существует производная Гато  оператора N, определяемая формулой

                              (1)

Решается задача существования вариационных принципов для заданных ДУЧП с отклоняющимися аргументами вида

       (2)

где -ограниченная область в, с кусочногладкой границей

в предположении достаточной гладкости всех рассматриваемых функций.

 Зададим область определения оператора N равенством

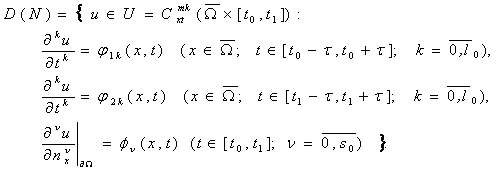    (3)

Здесь - заданные функции,  - неизвестная функция. Числа  зависят соответственно от . Если - четны, то При нечетном  полагаем    

Обозначим

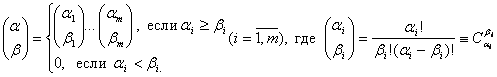
Введем классическую билинейную форму вида где                            (4)

Будем говорить, что уравнение (2) допускает прямую вариационную формулировку на множестве D(N), относительно билинейной формы (4), если существует функционал FN: D(FN )=D(N)—>R такой, что

   

Функционал FN называется потенциалом оператора N, а N – градиентом функционала FN. Записывают N=gradфFN. Оператор N называется потенциальным на множестве D(N) относительно Ф.

Обозначая через  замыкание области , будем предполагать, что - выпуклое множество, , для любых фиксированных элементов функция

Как известно [2., стр.15], необходимым и достаточным условием потенциальности оператора N на множестве D(N) относительно заданной формы является условие симметричности

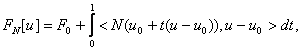Искомый функционал в этом случае имеет вид:

где F0 произвольный фиксированный элемент из R.

Для уравнения вида (2) устанавливается, что существует вариационный принцип в указанном выше смысле тогда и только тогда, когда справедлива

Теорема 1. Для потенциальности оператора (2) на множестве (3) относительно билинейной формы (4) необходимо и достаточно, чтобы выполнялись условия

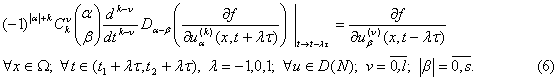
Современные качественные исследования устойчивости

Доказательство теоремы может быть проведено по схеме изложенной в работе [1, стр.43].

2.Примеры.

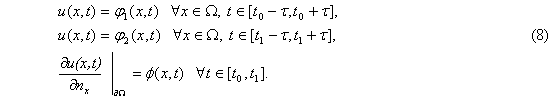А. Рассматривается дифференциальное уравнение с отклоняющимися аргументами вида (частный случай уравнения (2))

с граничными условиями

Для решения вопроса о вариационности задачи (7),(8) воспользуемся теоремой 1. Из условий (6) получим

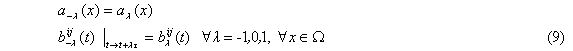
Отсюда заключаем, что в случае потенциальности рассматриваемого оператора коэффициенты a-1, a 0 ,a 1 могут зависеть только от x, а b-1, b0, b1 – только от t.

С учетом условий (9), уравнение (7) может быть записано в виде

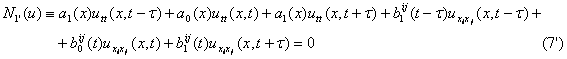
Таким образом, уравнение (7’) c граничными условиями (8) допускает вариационную формулировку.

Соответствующий функционал имеет вид

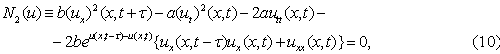В. Рассматривается уравнение

где a,b – const, u – неизвестная функция с граничными условиями

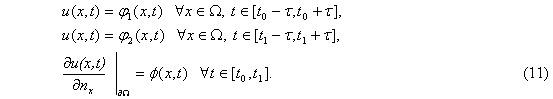
Для оператора задачи(10),(11) условия (6) не выполняются. В этой связи рассматривается следующая задача.

Найти функцию [2] М=М(x,t,u,ui) в Ω для любого u из D(N) и соответствующий функционал F[u] так, что

Используя условия (6), находим вариационный множитель М=еu(x,t). Тогда получим, что оператор вида

 

является потенциальным.

Соответствующее эквивалентное уравнение будет иметь вид:

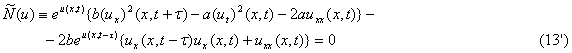
 Таким образом, задача (13’), (11) допускает вариационную формулировку с функционалом

Список литературы

 [1] Савчин В.М. Условия потенциальности Гельмгольца для ДУЧП с отклоняющимися аргументами.// XXXII Научная конференция факультета физико-математических и естественных наук. Тезисы докладов.1996г.С. 25.

[2] Филиппов В.М., Савчин В.М., Шорохов С.Г., Вариационные принципы для непотенциальных операторов. Итоги науки и техники. Современные проблемы математики. Новейшие достижения. Том 40.М.1992.

Для подготовки данной работы были использованы материалы с сайта http://ref.com.ua

Дата добавления: 05.03.2007