Химрастворы решают геометрию

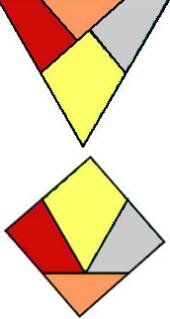
Разрежьте квадрат на четыре части так, чтобы собрать из них треугольник. Подобные геометрические задачи в свое время увлекали китайских ученых. Теперь химики создали наборы, которые сами собираются таким образом – в растворе. Этот трюк пригодится при создании самоорганизующихся контуров.

Разрежьте квадрат на четыре части так, чтобы собрать из них треугольник. Подобные геометрические задачи в свое время увлекали китайских ученых. Теперь химики создали наборы, которые сами собираются таким образом – в растворе. Этот трюк пригодится при создании самоорганизующихся контуров.

•	Геометрические задачи решаются в растворах

Джордж Вайтсайдс из Гарварда и его коллеги обработали края находящихся в жидкости полигональных фигур таким образом, что они сами соединяются в определенном порядке. Когда в жидкость, в которой плавают фигуры, добавляется соль, они разъединяются, а затем собираются в новом порядке. Сначала они скрепляются длинными гранями, образуя шестиугольники, а после перестройки соединяются короткими гранями, образуя равносторонние треугольники.

Для решения задачи превращения четырехугольника в треугольник потребовалась помощь людей. Четыре фрагмента разной формы были соединены хлопковой нитью, чтобы они не могли разбежаться или соединиться в неправильной последовательности. С такими ограничениями соль справлялась с задачей без проблем.

Фрагменты этого своеобразного паззла были изготовлены из водоотталкивающего полимера, смешанного с минеральным порошком. Они притягивают друг друга в результате действия капиллярных сил, благодаря которым, например, слипаются мокрые волосы. Ученые обработали грани фрагментов, чтобы они притягивали или отталкивали воду и друг друга. Похожие грани притягивали друг друга, разные отталкивались. Для контроля того, какая из сил доминирует, исследователи использовали плотность раствора: фрагменты обладали плотностью, которая позволяла им перемещаться между двумя несмешиваемыми жидкостями - водой и перхлородекалином. Когда фрагменты вытеснялись во вторую жидкость, они соединялись притягивающими воду гранями.

Добавление в воду соли делало ее плотнее, так что фрагменты немного приподнимались из перхлордекалина и тогда притяжение образовывалось между водоотталкивающими гранями. Однако таким способом не получится решить сложные геометрические головоломки – чтобы ответ получился правильным, грани заранее должны быть подогнаны. Но организация множества мелких объектов может иметь и практические применения. Подобные технологии, например, могут применяться при создании самоорганизующихся электронных схем.